Ohmov zákon je základným zákonom elektrických obvodov. Zároveň nám umožňuje vysvetliť mnohé prírodné javy. Dá sa napríklad pochopiť, prečo elektrina „nebije“vtáky, ktoré sedia na drôtoch. Pre fyziku je Ohmov zákon mimoriadne významný. Bez jeho vedomia by nebolo možné vytvoriť stabilné elektrické obvody alebo by neexistovala žiadna elektronika.
Závislosť I=I(U) a jej hodnota
História objavu odolnosti materiálov priamo súvisí s charakteristikou prúdového napätia. Čo to je? Zoberme si obvod s konštantným elektrickým prúdom a uvažujme ktorýkoľvek z jeho prvkov: lampa, plynové potrubie, kovový vodič, banka s elektrolytom atď.
Zmenou napätia U (často označovaného ako V) privádzaného do príslušného prvku budeme sledovať zmenu intenzity prúdu (I), ktorý ním prechádza. V dôsledku toho dostaneme závislosť formy I \u003d I (U), ktorá sa nazýva „napäťová charakteristika prvku“a je priamym ukazovateľom jehoelektrické vlastnosti.
V/A charakteristika môže pre rôzne prvky vyzerať odlišne. Jeho najjednoduchšiu formu získame zvážením kovového vodiča, ktorý vytvoril Georg Ohm (1789 - 1854).
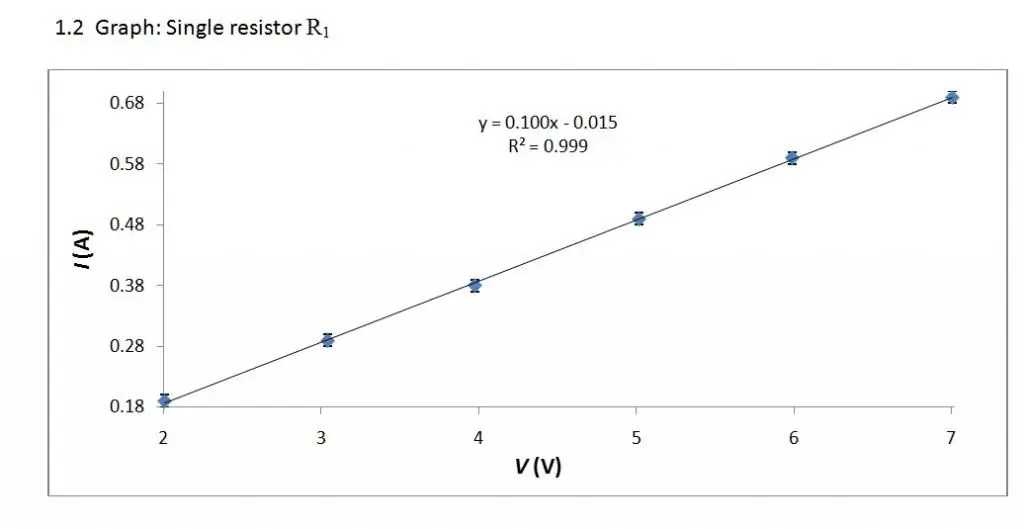
Volt-ampérová charakteristika je lineárny vzťah. Preto je jeho graf priamka.
Zákon v jeho najjednoduchšej podobe
Ohmov výskum charakteristík prúdového napätia vodičov ukázal, že sila prúdu vo vnútri kovového vodiča je úmerná potenciálnemu rozdielu na jeho koncoch (I ~ U) a nepriamo úmerná určitému koeficientu, tj I. ~ 1/R. Tento koeficient sa stal známym ako „odpor vodiča“a jednotka merania elektrického odporu bola Ohm alebo V/A.
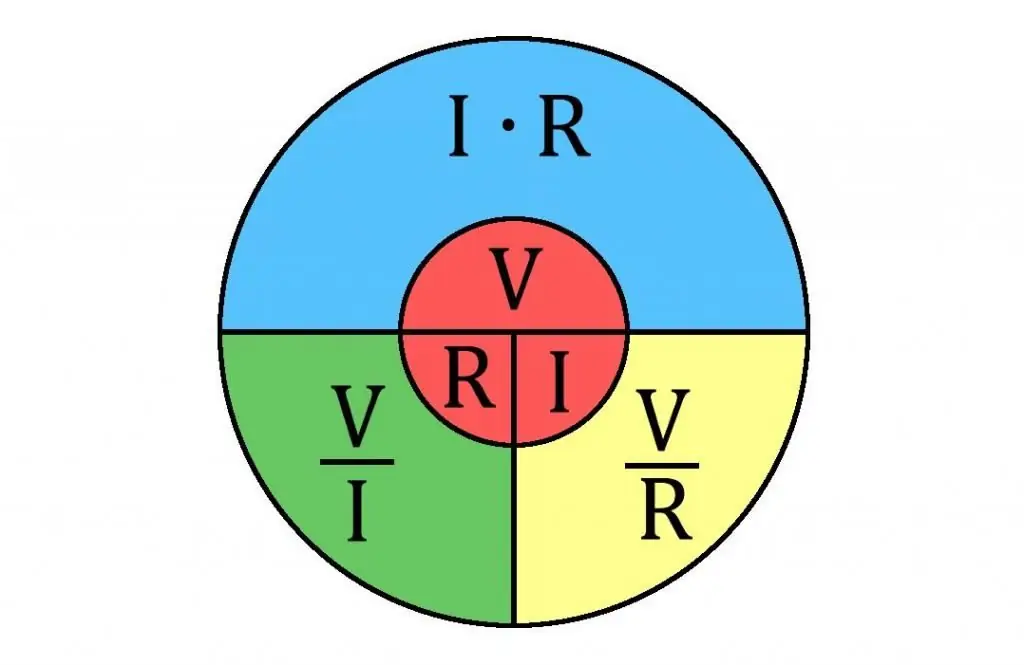
Je potrebné poznamenať ešte jednu vec. Ohmov zákon sa často používa na výpočet odporu v obvodoch.
Znenie zákona
Ohmov zákon hovorí, že sila prúdu (I) jednej časti obvodu je úmerná napätiu v tejto časti a nepriamo úmerná jej odporu.
Treba poznamenať, že v tejto podobe platí zákon len pre homogénnu časť reťazca. Homogénna je tá časť elektrického obvodu, ktorá neobsahuje zdroj prúdu. Ako používať Ohmov zákon v nehomogénnom obvode bude diskutované nižšie.
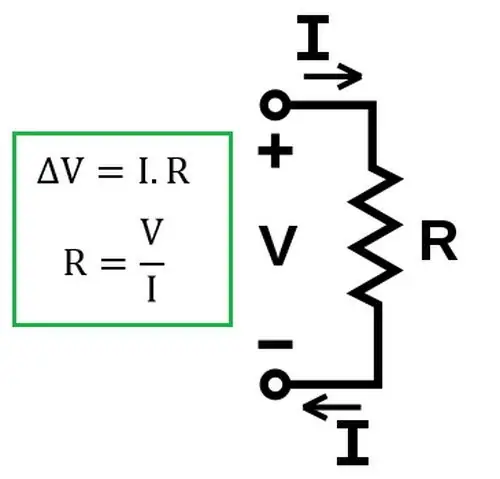
Neskôr sa experimentálne zistilo, že zákon zostáva platný pre riešeniaelektrolytov v elektrickom obvode.
Fyzický význam odporu
Odpor je vlastnosť materiálov, látok alebo médií brániť prechodu elektrického prúdu. Kvantitatívne znamená odpor 1 ohm, že vodičom s napätím 1 V na jeho koncoch môže prejsť elektrický prúd 1 A.
Elektrický odpor
Experimentálne sa zistilo, že odpor elektrického prúdu vodiča závisí od jeho rozmerov: dĺžka, šírka, výška. A tiež na jeho tvare (guľa, valec) a materiáli, z ktorého je vyrobený. Vzorec pre merný odpor, napríklad homogénneho valcového vodiča, bude teda: R \u003d pl / S.
Ak do tohto vzorca dáme s=1 m2 a l=1 m, potom sa R bude číselne rovnať p. Odtiaľto sa vypočíta merná jednotka pre koeficient odporu vodiča v SI - toto je Ohmm.

Vo vzorci odporu je p koeficient odporu určený chemickými vlastnosťami materiálu, z ktorého je vodič vyrobený.
Ak chcete zvážiť diferenciálnu formu Ohmovho zákona, musíme zvážiť niekoľko ďalších konceptov.
Aktuálna hustota
Ako viete, elektrický prúd je striktne usporiadaný pohyb akýchkoľvek nabitých častíc. Napríklad v kovoch sú nosičmi prúdu elektróny a vo vodivých plynoch ióny.
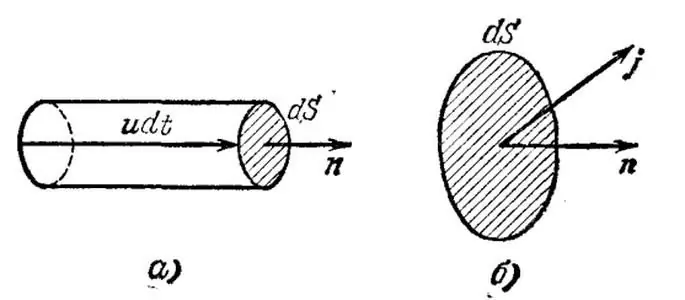
Vezmite si triviálny prípad, keď všetci súčasní operátorihomogénny - kovový vodič. V duchu vyčlenme nekonečne malý objem v tomto vodiči a označme u priemernú (drift, usporiadanú) rýchlosť elektrónov v danom objeme. Ďalej nech n označuje koncentráciu aktuálnych nosičov na jednotku objemu.
Teraz nakreslíme infinitezimálnu plochu dS kolmú na vektor u a zostrojíme pozdĺž rýchlosti nekonečne malý valec s výškou udt, kde dt označuje čas, počas ktorého prejdú všetky aktuálne nosiče rýchlosti obsiahnuté v uvažovanom objeme cez oblasť dS.
V tomto prípade náboj rovný q=neudSdt prenesú elektróny cez oblasť, kde e je náboj elektrónu. Hustota elektrického prúdu je teda vektor j=neu, ktorý označuje množstvo náboja preneseného za jednotku času cez jednotku plochy.
Jednou z výhod diferenciálnej definície Ohmovho zákona je, že sa často zaobídete bez výpočtu odporu.
Elektrický náboj. Sila elektrického poľa
Sila poľa spolu s elektrickým nábojom je základným parametrom v teórii elektriny. Zároveň o nich možno získať kvantitatívnu predstavu z jednoduchých experimentov dostupných školákom.
Pre jednoduchosť budeme uvažovať o elektrostatickom poli. Toto je elektrické pole, ktoré sa časom nemení. Takéto pole môžu vytvoriť stacionárne elektrické náboje.
Na naše účely je potrebné aj skúšobné nabitie. V jeho kapacite použijeme nabité telo - také malé, že nie je schopné spôsobiťakékoľvek poruchy (prerozdelenie nábojov) v okolitých objektoch.
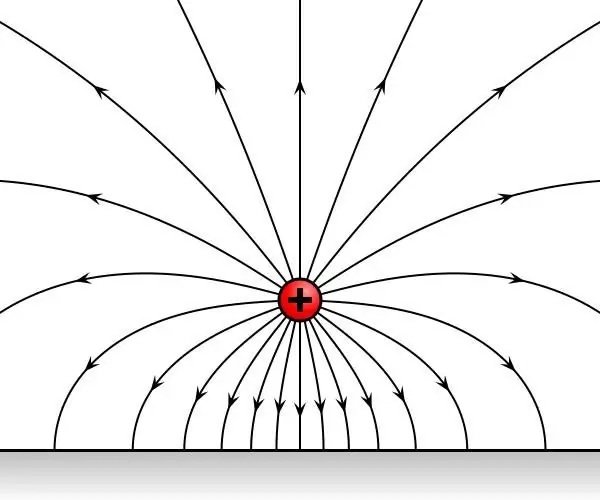
Uvažujme postupne o dvoch testovacích nábojoch, ktoré boli postupne umiestnené v jednom bode v priestore, ktorý je pod vplyvom elektrostatického poľa. Ukazuje sa, že obvinenia budú z jeho strany vystavené časovo nemennému vplyvu. Nech F1 a F2 sú sily pôsobiace na náboje.
Výsledkom zovšeobecnenia experimentálnych údajov sa zistilo, že sily F1 a F2 smerujú buď do jednej resp. v opačných smeroch a ich pomer F1/F2 je nezávislý od bodu v priestore, kde boli striedavo umiestnené testovacie náboje. Preto je pomer F1/F2 charakteristikou samotných poplatkov a nezávisí od poľa.
Odhalenie tejto skutočnosti umožnilo charakterizovať elektrizáciu telies a neskôr sa nazývalo elektrický náboj. Z definície teda vyplýva, že q1/q2=F1/F 2 , kde q1 a q2 - množstvo poplatkov uložených v jednom bode poľa a F 1 a F2 - sily pôsobiace na náboje zo strany poľa.
Na základe týchto úvah boli experimentálne stanovené veľkosti nábojov rôznych častíc. Podmienečným nastavením jedného z testovacích nábojov na jeden v pomere môžete vypočítať hodnotu druhého náboja meraním pomeru F1/F2.
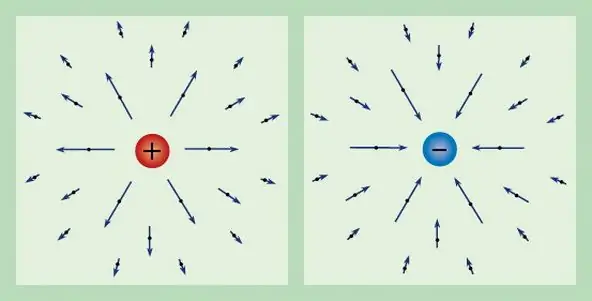
Akékoľvek elektrické pole možno charakterizovať pomocou známeho náboja. Sila pôsobiaca na jednotkový testovací náboj v pokoji sa teda nazýva intenzita elektrického poľa a označuje sa E. Z definície náboja dostaneme, že vektor sily má nasledujúci tvar: E=F/q.
Spojenie vektorov j a E. Iná forma Ohmovho zákona
V homogénnom vodiči nastane usporiadaný pohyb nabitých častíc v smere vektora E. To znamená, že vektory j a E budú smerované spoločne. Rovnako ako pri určovaní prúdovej hustoty volíme vo vodiči nekonečne malý valcový objem. Potom cez prierez tohto valca prejde prúd rovný jdS a napätie aplikované na valec sa bude rovnať Edl. Známy je aj vzorec pre merný odpor valca.
Potom napísaním vzorca pre intenzitu prúdu dvoma spôsobmi dostaneme: j=E/p, kde hodnota 1/p sa nazýva elektrická vodivosť a je inverznou hodnotou k elektrickému odporu. Zvyčajne sa označuje σ (sigma) alebo λ (lambda). Jednotkou vodivosti je Sm/m, kde Sm je Siemens. Jednotka inverzná k Ohm.
Takto môžeme odpovedať na vyššie položenú otázku o Ohmovom zákone pre nehomogénny obvod. V tomto prípade budú na prúdové nosiče pôsobiť sila z elektrostatického poľa, ktorá je charakterizovaná intenzitou E1 a ďalšie sily pôsobiace na ne z iného zdroja prúdu, ktorý môže byť označené E 2. Potom platil Ohmov zákonnehomogénny úsek reťazca bude vyzerať takto: j=λ(E1 + E2).
Viac o vodivosti a odpore
Schopnosť vodiča viesť elektrický prúd je charakterizovaná jeho merným odporom, ktorý možno zistiť pomocou vzorca merného odporu alebo vodivosti, vypočítanej ako prevrátená hodnota vodivosti. Hodnota týchto parametrov je určená jednak chemickými vlastnosťami materiálu vodiča a jednak vonkajšími podmienkami. Najmä teplota okolia.
Pre väčšinu kovov je merný odpor pri normálnej teplote úmerný tomu, to znamená p ~ T. Pri nízkych teplotách sa však pozorujú odchýlky. Pre veľké množstvo kovov a zliatin pri teplotách blízkych 0°K ukázal výpočet odporu nulové hodnoty. Tento jav sa nazýva supravodivosť. Túto vlastnosť má napríklad ortuť, cín, olovo, hliník atď.. Každý kov má svoju kritickú teplotu Tk, pri ktorej sa pozoruje fenomén supravodivosti.
Všimnite si tiež, že definíciu odporu valca možno zovšeobecniť na drôty vyrobené z rovnakého materiálu. V tomto prípade sa plocha prierezu zo vzorca odporu bude rovnať prierezu drôtu a l - jeho dĺžke.






