Existujú predmety, ktoré sú schopné meniť hustotu toku elektromagnetického žiarenia, ktoré na ne dopadá, to znamená buď ju zvyšovať zhromažďovaním v jednom bode, alebo zmenšovať jej rozptylom. Tieto objekty sa vo fyzike nazývajú šošovky. Pozrime sa na tento problém bližšie.
Čo sú šošovky vo fyzike?
Tento pojem znamená absolútne akýkoľvek objekt, ktorý je schopný zmeniť smer šírenia elektromagnetického žiarenia. Toto je všeobecná definícia šošoviek vo fyzike, ktorá zahŕňa optické okuliare, magnetické a gravitačné šošovky.
V tomto článku sa zameriame na optické sklá, čo sú predmety vyrobené z priehľadného materiálu a ohraničené dvoma povrchmi. Jeden z týchto povrchov musí mať nevyhnutne zakrivenie (to znamená, že musí byť súčasťou gule s konečným polomerom), inak objekt nebude mať vlastnosť meniť smer šírenia svetelných lúčov.
Princíp šošovky

Podstata práce tohto nekomplikovanéhooptický objekt je jav lomu slnečných lúčov. Začiatkom 17. storočia publikoval slávny holandský fyzik a astronóm Willebrord Snell van Rooyen zákon lomu, ktorý v súčasnosti nesie jeho priezvisko. Formulácia tohto zákona je nasledovná: keď slnečné svetlo prechádza rozhraním medzi dvoma opticky priehľadnými médiami, potom súčin sínusu uhla dopadu medzi lúčom a normálou k povrchu a indexu lomu prostredia, v ktorom šíri sa je konštantná hodnota.

Na objasnenie vyššie uvedeného uveďme príklad: nechajte svetlo dopadať na hladinu vody, pričom uhol medzi normálou k hladine a lúčom je θ1. Potom sa svetelný lúč láme a začína sa šíriť vo vode už pod uhlom θ2 k normále k povrchu. Podľa Snellovho zákona dostaneme: sin(θ1)n1=sin(θ2) n2, kde n1 a n2 sú indexy lomu vzduchu a vody, resp. Aký je index lomu? Toto je hodnota, ktorá ukazuje, koľkokrát je rýchlosť šírenia elektromagnetických vĺn vo vákuu väčšia ako rýchlosť pre opticky priehľadné prostredie, teda n=c/v, kde c a v sú rýchlosti svetla vo vákuu a v stredné, resp.
Fyzika vzhľadu lomu spočíva v implementácii Fermatovho princípu, podľa ktorého sa svetlo pohybuje tak, aby prekonalo vzdialenosť z jedného bodu do druhého v priestore za čo najkratší čas.
Typy šošoviek

Typ optickej šošovky vo fyzike je určený výlučne tvarom povrchov, ktoré ju tvoria. Od tohto tvaru závisí smer lomu lúča, ktorý na ne dopadá. Ak je teda zakrivenie povrchu kladné (konvexné), potom sa svetelný lúč pri výstupe z šošovky bude šíriť bližšie k svojej optickej osi (pozri nižšie). Naopak, ak je zakrivenie povrchu záporné (konkávne), potom sa lúč pri prechode cez optické sklo posunie od svojej stredovej osi.
Znova si všimnite, že povrch akéhokoľvek zakrivenia láme lúče rovnakým spôsobom (podľa Stellovho zákona), ale normály k nim majú odlišný sklon vzhľadom k optickej osi, čo má za následok odlišné správanie lomeného lúča.
Šošovka ohraničená dvoma konvexnými plochami sa nazýva zbiehavá šošovka. Na druhej strane, ak je tvorený dvoma povrchmi s negatívnym zakrivením, nazýva sa to rozptyl. Všetky ostatné typy optických skiel sú spojené s kombináciou týchto plôch, ku ktorým sa pridáva aj rovina. Akú vlastnosť bude mať kombinovaná šošovka (divergentná alebo konvergujúca) závisí od celkového zakrivenia polomerov jej povrchov.
Prvky šošovky a vlastnosti lúčov

Na zabudovanie šošoviek do fyziky obrazu sa musíte zoznámiť s prvkami tohto objektu. Sú uvedené nižšie:
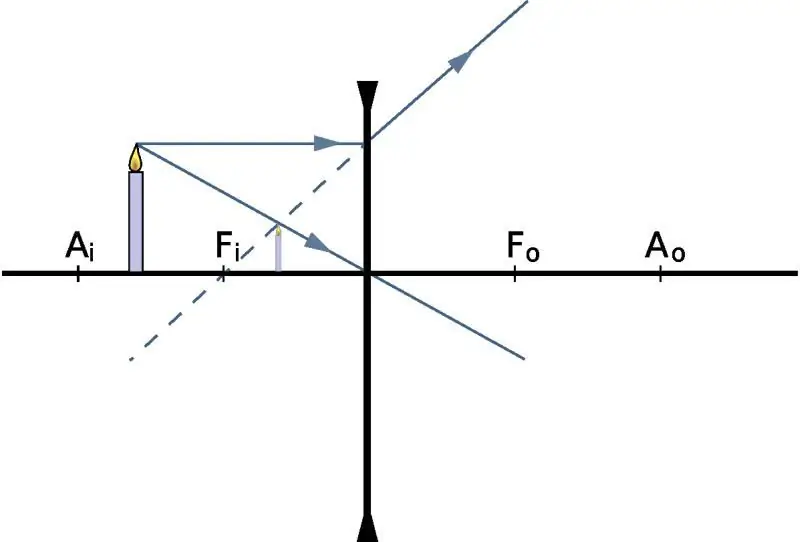
- Hlavná optická os a stred. V prvom prípade znamenajú priamku prechádzajúcu kolmo na šošovku cez jej optický stred. Ten je zasa bod vo vnútri šošovky, cez ktorý lúč neprechádza lomom.
- Ohnisková vzdialenosť a ohnisko - vzdialenosť medzi stredom a bodom na optickej osi, ktorý zbiera všetky lúče dopadajúce na šošovku rovnobežne s touto osou. Táto definícia platí pre zber optických skiel. V prípade divergentných šošoviek to nie sú samotné lúče, ktoré sa budú zbiehať do bodu, ale ich pomyselné pokračovanie. Tento bod sa nazýva hlavné zameranie.
- Optický výkon. Toto je názov prevrátenej ohniskovej vzdialenosti, to znamená D \u003d 1 / f. Meria sa v dioptriách (dioptriách), teda 1 dioptrii.=1 m-1.
Nasledujú hlavné vlastnosti lúčov, ktoré prechádzajú šošovkou:
- lúč prechádzajúci cez optický stred nemení smer svojho pohybu;
- lúče dopadajúce rovnobežne s hlavnou optickou osou menia svoj smer tak, že prechádzajú cez hlavné ohnisko;
- lúče dopadajúce na optické sklo pod ľubovoľným uhlom, ale prechádzajúce jeho ohniskom, menia svoj smer šírenia tak, že sa stávajú rovnobežnými s hlavnou optickou osou.
Vyššie uvedené vlastnosti lúčov pre tenké šošovky vo fyzike (ako sa im hovorí, pretože bez ohľadu na to, aké gule sú vytvorené a aké hrubé sú, záleží len na optických vlastnostiach objektu) sa používajú na vytváranie obrazov v nich.
Obrázky v optických okuliaroch: ako vytvoriť?
Nižšie je uvedený obrázok, ktorý podrobne popisuje schémy na vytváranie obrázkov v konvexných a konkávnych šošovkách objektu(červená šípka) v závislosti od jej polohy.
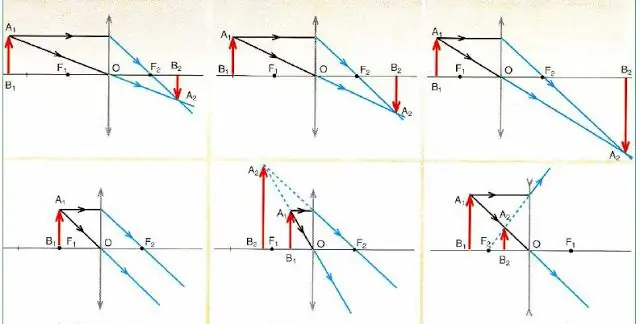
Z analýzy obvodov na obrázku vyplývajú dôležité závery:
- Každý obraz je postavený iba na 2 lúčoch (prechádzajúcich stredom a rovnobežne s hlavnou optickou osou).
- Zbiehavé šošovky (označené šípkami na koncoch smerujúcich von) môžu poskytnúť zväčšený aj zmenšený obraz, ktorý môže byť skutočný (skutočný) alebo imaginárny.
- Ak je objekt zaostrený, šošovka netvorí svoj obraz (pozri dolný diagram vľavo na obrázku).
- Rozptylové optické sklá (označené šípkami na ich koncoch smerujúcimi dovnútra) vždy poskytujú zmenšený a virtuálny obraz bez ohľadu na polohu objektu.
Hľadanie vzdialenosti k obrázku
Aby sme určili, v akej vzdialenosti sa obraz objaví, keďže poznáme polohu samotného objektu, dáme vo fyzike vzorec pre šošovky: 1/f=1/do + 1 /d i, kde do a di sú vzdialenosť k objektu a k jeho obrazu z optiky stred, respektíve f je hlavným zameraním. Ak hovoríme o zbernom optickom skle, potom bude clonové číslo kladné. Naopak, pre divergentnú šošovku je f záporné.
Použime tento vzorec a vyriešme jednoduchý problém: nech je objekt vo vzdialenosti do=2f od stredu zberného optického skla. Kde sa objaví jeho obrázok?
Z podmienok problému máme: 1/f=1/(2f)+1/di. Od: 1/di=1/f - 1/(2f)=1/(2f), t. j. di=2 f. Obraz sa teda objaví vo vzdialenosti dvoch ohnísk od šošovky, ale na druhej strane ako samotný objekt (označuje to kladné znamienko hodnoty di).
Stručná história
Je zaujímavé uviesť etymológiu slova „šošovka“. Pochádza z latinských slov lens a lentis, čo znamená „šošovica“, keďže optické objekty svojím tvarom skutočne vyzerajú ako plody tejto rastliny.
Sila lomu sférických priehľadných telies bola známa už starým Rimanom. Na tento účel používali okrúhle sklenené nádoby naplnené vodou. Samotné sklenené šošovky sa v Európe začali vyrábať až v 13. storočí. Používali sa ako nástroj na čítanie (moderné okuliare alebo lupa).
Aktívne používanie optických predmetov pri výrobe ďalekohľadov a mikroskopov siaha až do 17. storočia (začiatkom tohto storočia vynašiel prvý ďalekohľad Galileo). Všimnite si, že matematickú formuláciu Stellovho zákona lomu, bez znalosti ktorého nie je možné vyrobiť šošovky s požadovanými vlastnosťami, zverejnil holandský vedec na začiatku toho istého 17. storočia.
Iné šošovky
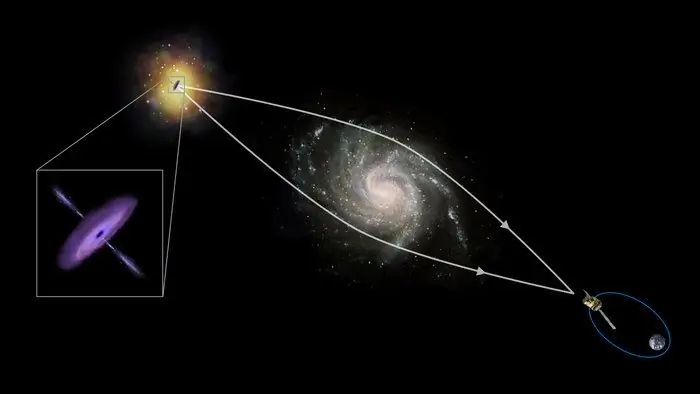
Ako je uvedené vyššie, okrem optických refrakčných objektov existujú aj magnetické a gravitačné objekty. Príkladom prvého sú magnetické šošovky v elektrónovom mikroskope, živým príkladom druhého je skreslenie smeru svetelného toku,keď prechádza blízko masívnych vesmírnych telies (hviezd, planét).






