Titiovo-Bodeho pravidlo (niekedy jednoducho nazývané Bodeov zákon) je hypotéza, že telesá v niektorých orbitálnych systémoch vrátane Slnka rotujú pozdĺž poloosí v závislosti od planetárnej postupnosti. Vzorec naznačuje, že pri predĺžení smerom von bude každá planéta približne dvakrát tak ďaleko od Slnka ako predchádzajúca.
Hypotéza správne predpovedala obežné dráhy Ceres (v páse asteroidov) a Uránu, ale nepodarilo sa jej určiť obežnú dráhu Neptúna a nakoniec bola nahradená teóriou formovania slnečnej sústavy. Je pomenovaná po Johannovi Danielovi Titiusovi a Johannovi Elertovi Bodemu.

Origins
Prvú zmienku o sérii, ktorá sa približuje Bodeovmu zákonu, možno nájsť v knihe Davida Gregoryho Elements of Astronomy, publikovanej v roku 1715. V ňom hovorí: „… za predpokladu, že vzdialenosť od Slnka k Zemi je rozdelená na desať rovnakých častí, z ktorých vzdialenosť Merkúra bude asi štyri, od Venuše sedem, od Marsu pätnásť, od Jupitera päťdesiatdva, a od Saturnu deväťdesiatpäť“. Podobný návrh, pravdepodobne inšpirovaný Gregorom, sa objavuje v diele, ktoré vydal Christian Wolff v roku 1724.
V roku 1764 Charles Bonnet vo svojej knihe Contemplation of Nature povedal: „Poznáme sedemnásť planét, ktoré tvoria našu slnečnú sústavu [to znamená hlavné planéty a ich satelity], ale nie sme si istí, či už nie sú." Johann Daniel Titius vo svojom preklade Bonnetovho diela z roku 1766 pridal dva vlastné odseky na spodok strany 7 a na začiatok strany 8. Nový interpolovaný odsek sa v Bonnetovom pôvodnom texte nenachádza: ani v talianskom ani anglické preklady diela.
Objavenie Titia
V interkalovanom Titiusovom texte sú dve časti. Prvá vysvetľuje postupnosť vzdialeností planét od Slnka. Obsahuje aj pár slov o vzdialenosti od Slnka k Jupiteru. Toto však nie je koniec textu.
Stojí za to povedať pár slov o vzorci Titius-Bodeho pravidla. Všímajte si vzdialenosti medzi planétami a zistite, že takmer všetky sú od seba oddelené v pomere zodpovedajúcom ich telesným veľkostiam. Vydeľte vzdialenosť od Slnka k Saturnu 100 dielmi; potom je Merkúr oddelený štyrmi takými časťami od Slnka; Venuša - na 4 + 3=7 takýchto častí; Zem - o 4+6=10; Mars - o 4+12=16.
Všimnite si však, že od Marsu k Jupiteru existuje odchýlka od tohto tak presného postupu. Z Marsu nasleduje priestor 4+24=28 takýchto častí, ale zatiaľ tam nebola objavená ani jedna planéta. Mal by však Pán architekt nechať toto miesto prázdne? Nikdy. Takžepredpokladajme, že tento priestor bezpochyby patrí k zatiaľ neobjaveným mesiacom Marsu, a dodajme, že možno má Jupiter okolo seba ešte niekoľko menších mesiacov, ktoré ešte nevidel žiadny ďalekohľad.

Rise of the Bode
V roku 1772 Johann Elert Bode vo veku dvadsaťpäť rokov dokončil druhé vydanie svojho astronomického kompendia Anleitung zur Kenntniss des gestirnten Himmels („Sprievodca poznaním hviezdnej oblohy“), ku ktorému pridala nasledujúcu poznámku pod čiarou, pôvodne bez zdroja, ale uvedená v neskorších verziách. V Bodeových memoároch možno nájsť zmienku o Titiovi s jasným uznaním jeho autority.

Opinion Bode
Takto znie Titiusovo-Bodeho pravidlo v jeho podaní: ak sa vzdialenosť od Slnka k Saturnu rovná 100, potom je Merkúr oddelený od Slnka štyrmi takýmito časťami. Venuša - 4+3=7. Zem - 4+6=10. Mars - 4+12=16.
Teraz je v tomto usporiadanom postupe medzera. Po Marse nasleduje priestor s výpočtom 4+24=28, v ktorom ešte nebola videná ani jedna planéta. Môžeme uveriť, že zakladateľ vesmíru nechal tento priestor prázdny? Samozrejme, že nie. Odtiaľ sa dostávame k vzdialenosti Jupitera vo forme výpočtu 4+48=52 a nakoniec k vzdialenosti Saturna - 4+96=100.

Tieto dve vyhlásenia týkajúce sa všetkých špecifických typológií a orbitálnych polomerov zrejme pochádzajú zo starovekuastronómia. Mnohé z týchto teórií sa datujú pred sedemnáste storočie.
Vplyv
Titius bol žiakom nemeckého filozofa Christiana Freiherra von Wolffa (1679-1754). Druhá časť vloženého textu v Bonnetovom diele vychádza z von Wolffovho diela z roku 1723, Vernünftige Gedanken von den Wirkungen der Natur.
Literatúra dvadsiateho storočia pripisuje autorstvo Titius-Bodeho vlády nemeckému filozofovi. Ak áno, Titius by sa od neho mohol učiť. Ďalší starší odkaz napísal James Gregory v roku 1702 vo svojom diele Astronomiae Physicae et geometryae Elementa, kde sa postupnosť planetárnych vzdialeností 4, 7, 10, 16, 52 a 100 stala geometrickou progresiou pomeru 2.
Toto je Newtonov najbližší vzorec a bol tiež nájdený v spisoch Benjamina Martina a Thomasa Cearda roky pred vydaním Bonnetovej knihy v Nemecku.
Ďalšia práca a praktické dôsledky
Titius a Bode dúfali, že zákon povedie k objavu nových planét, a skutočne, objav Uránu a Ceres, ktorých vzdialenosť je v súlade so zákonom, prispel k jeho prijatiu vedeckým svetom.
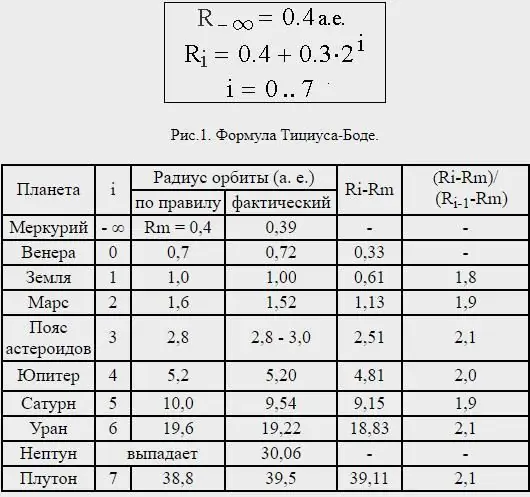
Vzdialenosť Neptúna však bola veľmi nekonzistentná av skutočnosti je Pluto - teraz nepovažované za planétu - v priemernej vzdialenosti, ktorá zhruba zodpovedá Titius-Bodeovmu zákonu predpovedanému pre ďalšiu planétu mimo Uránu.
Pôvodne publikovanému zákonu vyhoveli približne všetky známe planéty - Merkúr a Saturn - s medzerou medzištvrtá a piata planéta. Až do objavenia Uránu v roku 1781 sa to považovalo za zaujímavú, ale nie veľmi dôležitú postavu, ktorá zapadá do série.
Na základe tohto objavu Bode vyzval na hľadanie piatej planéty. Ceres, najväčší objekt v páse asteroidov, bol nájdený v Bodeovej predpovedanej polohe v roku 1801. Bodeov zákon bol široko akceptovaný, kým v roku 1846 nebol objavený Neptún a nepreukázalo sa, že je v rozpore so zákonom.
V tom istom čase veľké množstvo asteroidov objavených v páse prekročilo Ceres zo zoznamu planét. Bodeov zákon diskutoval astronóm a logik Charles Sanders Peirce v roku 1898 ako príklad mylného uvažovania.

Vývoj problému
Objav Pluta v roku 1930 problém ešte viac skomplikoval. Aj keď sa to nezhodovalo s polohou, ktorú predpovedal Bodeov zákon, išlo o polohu, ktorú zákon predpovedal pre Neptún. Následný objav Kuiperovho pásu a najmä objektu Eris, ktorý je masívnejší ako Pluto, no nevyhovuje Bodeovmu zákonu, však vzorec ešte viac zdiskreditoval.
Serdov príspevok
Jezuita Thomas Cerda viedol slávny kurz astronómie v Barcelone v roku 1760 na Royal Chair of Mathematics na College of Sant Jaume de Cordelle (Imperial and Royal Seminary of the Nobles of Cordell). V Cerdasovom Tratado sa objavujú planetárne vzdialenosti získané aplikáciou tretieho Keplerovho zákona s presnosťou 10-3.
Ak vezmeme ako 10 vzdialenosť od Zeme azaokrúhliť nahor na celé číslo, možno vyjadriť geometrickú postupnosť [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, od n=2 do n=8. A pomocou kruhového rovnomerného fiktívneho pohybu na Keplerovu anomáliu možno hodnoty Rn zodpovedajúce pomerom každej planéty získať ako rn=(Rn - R1) / (Rn-1 - R1), čo vedie k 1,82; 1,84; 1,86; 1,88 a 1,90, kde rn=2 - 0,02 (12 - n) je explicitný vzťah medzi Keplerovou kontinuitou a Titius-Bodeovým zákonom, ktorý sa považuje za náhodnú číselnú zhodu. Výsledok výpočtu sa blíži k dvom, ale dvojku možno považovať za zaokrúhlenie čísla 1, 82.

Priemerná rýchlosť planéty z n=1 na n=8 znižuje vzdialenosť od Slnka a líši sa od rovnomerného poklesu pri n=2, aby sa zotavila z n=7 (orbitálna rezonancia). To ovplyvňuje vzdialenosť od Slnka k Jupiteru. Táto matematická dynamika však určuje aj vzdialenosť medzi všetkými ostatnými objektmi v rámci notoricky známeho pravidla, ktorému je venovaný článok.
Teoretický aspekt
Neexistuje žiadne solídne teoretické vysvetlenie, ktoré by bolo základom Titius-Bodeho pravidla, ale je možné, že vzhľadom na kombináciu orbitálnej rezonancie a nedostatku stupňov voľnosti má každý stabilný planetárny systém vysokú pravdepodobnosť zopakovania modelu opísaného v túto teóriu dvoch vedcov.
Pretože to môže byť matematická zhoda okolností a nie „zákon prírody“, niekedy sa to nazýva skôr pravidlo ako „zákon“. Astrofyzik Alan Boss však tvrdí, že je to jednoduchonáhoda a planetárny vedecký časopis Icarus už neprijíma články pokúšajúce sa poskytnúť vylepšené verzie „zákona“.
Orbitálna rezonancia
Orbitálna rezonancia z hlavných obiehajúcich telies vytvára okolo Slnka oblasti, ktoré nemajú dlhodobo stabilné obežné dráhy. Výsledky simulácie formovania planét podporujú myšlienku, že náhodne vybraný stabilný planetárny systém bude pravdepodobne spĺňať pravidlo Titius-Bode.

Dubrulle and Graner
Dubrulle a Graner ukázali, že mocninové pravidlá vzdialenosti môžu byť dôsledkom modelov kolabujúcich oblakov planetárnych systémov, ktoré majú dve symetrie: rotačnú invarianciu (oblak a jeho obsah sú osovo symetrické) a mierkovú invarianciu (oblaky a jeho obsah vyzerá na všetkých mierkach rovnako).
Ten druhý je znakom mnohých javov, o ktorých sa predpokladá, že zohrávajú úlohu pri formovaní planét, ako je napríklad turbulencia. Vzdialenosť od Slnka k planétam slnečnej sústavy, ktorú navrhli Titius a Bode, nebola revidovaná v rámci štúdií Dubrulleho a Granera.






