Svet, v ktorom žijeme, je nepredstaviteľne krásny a plný mnohých rôznych procesov, ktoré určujú smer života. Všetky tieto procesy študuje známa veda - fyzika. Poskytuje príležitosť získať aspoň nejakú predstavu o pôvode vesmíru. V tomto článku sa budeme zaoberať takou koncepciou, ako je molekulárna kinetická teória, jej rovnice, typy a vzorce. Avšak skôr, ako prejdete k hlbšiemu štúdiu týchto problémov, musíte si ujasniť samotný význam fyziky a oblastí, ktoré študuje.
Čo je fyzika?

V skutočnosti ide o veľmi rozsiahlu vedu a možno jednu z najzákladnejších v dejinách ľudstva. Napríklad, ak je tá istá informatika spojená s takmer každou oblasťou ľudskej činnosti, či už ide o výpočtový dizajn alebo tvorbu karikatúr, potom je fyzika životom samotným, popisom jeho zložitých procesov a tokov. Pokúsme sa pochopiť jeho význam a čo najviac zjednodušiť pochopenie.
TakžeFyzika je teda veda, ktorá sa zaoberá štúdiom energie a hmoty, súvislosťami medzi nimi, vysvetľovaním mnohých procesov prebiehajúcich v našom obrovskom vesmíre. Molekulárno-kinetická teória štruktúry hmoty je len malou kvapkou v mori teórií a odvetví fyziky.
Energia, ktorú táto veda podrobne študuje, môže byť zastúpená v rôznych formách. Napríklad v podobe svetla, pohybu, gravitácie, žiarenia, elektriny a mnohých iných foriem. V tomto článku sa dotkneme molekulárnej kinetickej teórie štruktúry týchto foriem.
Štúdium hmoty nám dáva predstavu o atómovej štruktúre hmoty. Mimochodom, vyplýva to z molekulárno-kinetickej teórie. Veda o štruktúre hmoty nám umožňuje pochopiť a nájsť zmysel našej existencie, dôvody vzniku života a samotného Vesmíru. Skúsme ešte študovať molekulárnu kinetickú teóriu hmoty.
Najprv je potrebný úvod na úplné pochopenie terminológie a akýchkoľvek záverov.
Fyzikálne témy
Pri odpovedi na otázku, čo je molekulárno-kinetická teória, nemožno hovoriť o úsekoch fyziky. Každý z nich sa zaoberá podrobným štúdiom a vysvetlením konkrétnej oblasti ľudského života. Sú klasifikované takto:
- Mechanika, ktorá je rozdelená na ďalšie dve sekcie: kinematika a dynamika.
- Statické.
- Termodynamika.
- Molekulárna sekcia.
- Elektrodynamika.
- Optika.
- Fyzika kvánt a atómového jadra.
Poďme hovoriť konkrétne o molekulárnejfyzika, pretože je založená na molekulárno-kinetickej teórii.
Čo je termodynamika?
Vo všeobecnosti sú molekulárna časť a termodynamika úzko súvisiace oblasti fyziky, ktoré študujú výlučne makroskopickú zložku celkového počtu fyzikálnych systémov. Stojí za to pripomenúť, že tieto vedy presne opisujú vnútorný stav tiel a látok. Napríklad ich stav počas zahrievania, kryštalizácie, odparovania a kondenzácie, na úrovni atómov. Inými slovami, molekulárna fyzika je veda o systémoch, ktoré pozostávajú z obrovského počtu častíc: atómov a molekúl.
Boli to tieto vedy, ktoré študovali hlavné ustanovenia molekulárnej kinetickej teórie.
Už v priebehu siedmeho ročníka sme sa zoznamovali s pojmami mikro- a makrosvety, systémy. Nebude zbytočné obnovovať si tieto výrazy v pamäti.
Mikrosvet, ako môžeme vidieť už z jeho názvu, tvoria elementárne častice. Inými slovami, toto je svet malých častíc. Ich veľkosti sa merajú v rozsahu od 10-18 m do 10-4 m a čas ich skutočného stavu môže dosiahnuť nekonečno aj neúmerne malé intervaly, napríklad 10-20 s.
Makrosvet uvažuje o telách a systémoch stabilných foriem, ktoré pozostávajú z mnohých elementárnych častíc. Takéto systémy sú úmerné našej ľudskej veľkosti.
Okrem toho existuje niečo ako megasvet. Skladá sa z obrovských planét, kozmických galaxií a komplexov.
Základyteória
Teraz, keď sme si to trochu zrekapitulovali a zapamätali si základné pojmy fyziky, môžeme prejsť priamo k hlavnej téme tohto článku.
Molekulárno-kinetická teória sa objavila a bola prvýkrát sformulovaná v devätnástom storočí. Jeho podstata spočíva v tom, že podrobne popisuje štruktúru akejkoľvek látky (častejšie štruktúru plynov ako pevných a kvapalných telies), na základe troch základných ustanovení, ktoré boli zozbierané z predpokladov takých významných vedcov ako Robert Hooke, Isaac Newton, Daniel Bernoulli, Michail Lomonosov a mnohí ďalší.
Hlavné ustanovenia molekulárnej kinetickej teórie znejú takto:
- Absolútne všetky látky (bez ohľadu na to, či sú kvapalné, pevné alebo plynné) majú zložitú štruktúru pozostávajúcu z menších častíc: molekúl a atómov. Atómy sa niekedy nazývajú „elementárne molekuly“.
- Všetky tieto elementárne častice sú vždy v stave nepretržitého a chaotického pohybu. Každý z nás sa stretol s priamym dôkazom tohto tvrdenia, ale s najväčšou pravdepodobnosťou mu neprikladal veľký význam. Všetci sme napríklad na pozadí slnečných lúčov videli, že prachové častice sa neustále pohybujú chaotickým smerom. Je to spôsobené tým, že atómy sa navzájom tlačia, pričom si navzájom neustále odovzdávajú kinetickú energiu. Tento jav bol prvýkrát študovaný v roku 1827 a bol pomenovaný po objaviteľovi - „Brownov pohyb“.
- Všetky elementárne častice sú v procese neustálej vzájomnej interakcieurčité sily, ktoré majú elektrický kameň.
Za zmienku stojí, že ďalším príkladom popisujúcim polohu číslo dva, ktorý môže platiť napríklad aj pre molekulárnu kinetickú teóriu plynov, je difúzia. Stretávame sa s ním v každodennom živote a pri viacerých testoch a kontrolách, preto je dôležité mať o ňom predstavu.
Najprv zvážte nasledujúce príklady:
Lekár omylom vylial alkohol z fľaše na stôl. Alebo vám možno spadol flakón s parfumom a rozlial sa po celej podlahe.
Prečo v týchto dvoch prípadoch vôňa alkoholu aj vôňa parfumu po určitom čase zaplní celú miestnosť, a nielen oblasť, kde sa obsah týchto látok rozlial?
Odpoveď je jednoduchá: difúzia.
Difúzia - čo to je? Ako to tečie?

Toto je proces, pri ktorom častice, ktoré tvoria jednu konkrétnu látku (zvyčajne plyn), prenikajú do medzimolekulových dutín inej látky. V našich príkladoch vyššie sa stalo nasledovné: v dôsledku tepelného, to znamená nepretržitého a disociovaného pohybu, molekuly alkoholu a / alebo parfumu spadli do medzier medzi molekulami vzduchu. Postupne sa vplyvom kolízie s atómami a molekulami vzduchu šíria po miestnosti. Mimochodom, intenzita difúzie, teda rýchlosť jej prúdenia, závisí od hustoty látok zapojených do difúzie, ako aj od energie pohybu ich atómov a molekúl, nazývanej kinetická. Čím väčšia je kinetická energia, tým vyššia je rýchlosť týchto molekúl a ich intenzita.
Najrýchlejší proces difúzie možno nazvať difúzia v plynoch. Je to spôsobené tým, že plyn nie je homogénny vo svojom zložení, čo znamená, že medzimolekulové dutiny v plynoch zaberajú značné množstvo priestoru a proces získavania atómov a molekúl cudzej látky do nich prebieha ľahšie a rýchlejšie..
Tento proces je v kvapalinách trochu pomalší. Rozpustenie kociek cukru v hrnčeku čaju je len príkladom difúzie pevnej látky v kvapaline.
Najdlhší čas je však difúzia v telesách s pevnou kryštalickou štruktúrou. Je to presne tak, pretože štruktúra pevných látok je homogénna a má pevnú kryštálovú mriežku, v ktorej bunkách kmitajú atómy pevnej látky. Napríklad, ak sú povrchy dvoch kovových tyčí dobre vyčistené a potom sa navzájom dostanú do kontaktu, potom po dostatočne dlhom čase budeme schopní odhaliť kúsky jedného kovu v druhom a naopak.
Ako každá iná základná časť, základná teória fyziky je rozdelená na samostatné časti: klasifikácia, typy, vzorce, rovnice atď. Tak sme sa naučili základy molekulárnej kinetickej teórie. To znamená, že môžete pokojne prejsť k úvahám o jednotlivých teoretických blokoch.
Molekulárno-kinetická teória plynov
Je potrebné porozumieť ustanoveniam teórie plynov. Ako sme už povedali, zvážime makroskopické charakteristiky plynov, ako je tlak a teplota. Toto jebudú potrebné neskôr na odvodenie rovnice molekulárno-kinetickej teórie plynov. Ale matematika - neskôr a teraz sa poďme zaoberať teóriou, a teda fyzikou.
Vedci sformulovali päť ustanovení molekulárnej teórie plynov, ktoré slúžia na pochopenie kinetického modelu plynov. Znejú takto:
- Všetky plyny sú tvorené elementárnymi časticami, ktoré nemajú určitú veľkosť, ale majú určitú hmotnosť. Inými slovami, objem týchto častíc je minimálny v porovnaní s dĺžkou medzi nimi.
- Atómy a molekuly plynov nemajú prakticky žiadnu potenciálnu energiu, respektíve podľa zákona sa všetka energia rovná kinetickej.
- S touto pozíciou sme sa už zoznámili skôr - Brownov pohyb. To znamená, že častice plynu sú vždy v nepretržitom a chaotickom pohybe.
- Absolútne všetky vzájomné zrážky častíc plynu sprevádzané posolstvom rýchlosti a energie sú úplne elastické. To znamená, že počas kolízie nedochádza k strate energie ani prudkým skokom v ich kinetickej energii.
- Pri normálnych podmienkach a konštantnej teplote je priemerná energia pohybu častíc takmer všetkých plynov rovnaká.
Piatu pozíciu môžeme prepísať cez tento typ rovnice molekulárno-kinetickej teórie plynov:
E=1/2mv^2=3/2kT, kde k je Boltzmannova konštanta; T - teplota v Kelvinoch.
Táto rovnica nám umožňuje pochopiť vzťah medzi rýchlosťou elementárnych častíc plynu a ich absolútnou teplotou. V súlade s tým, čím vyššia je ich absolútnateplota, tým väčšia je ich rýchlosť a kinetická energia.
Tlak plynu
Takéto makroskopické zložky charakteristiky, ako je tlak plynov, možno vysvetliť aj pomocou kinetickej teórie. Aby sme to urobili, predstavme si nasledujúci príklad.
Predpokladajme, že molekula nejakého plynu je v krabici, ktorej dĺžka je L. Využime ustanovenia plynovej teórie opísanej vyššie a vezmime do úvahy skutočnosť, že molekulárna guľa sa pohybuje iba po x -os. Budeme tak môcť pozorovať proces elastickej kolízie s jednou zo stien nádoby (boxu).
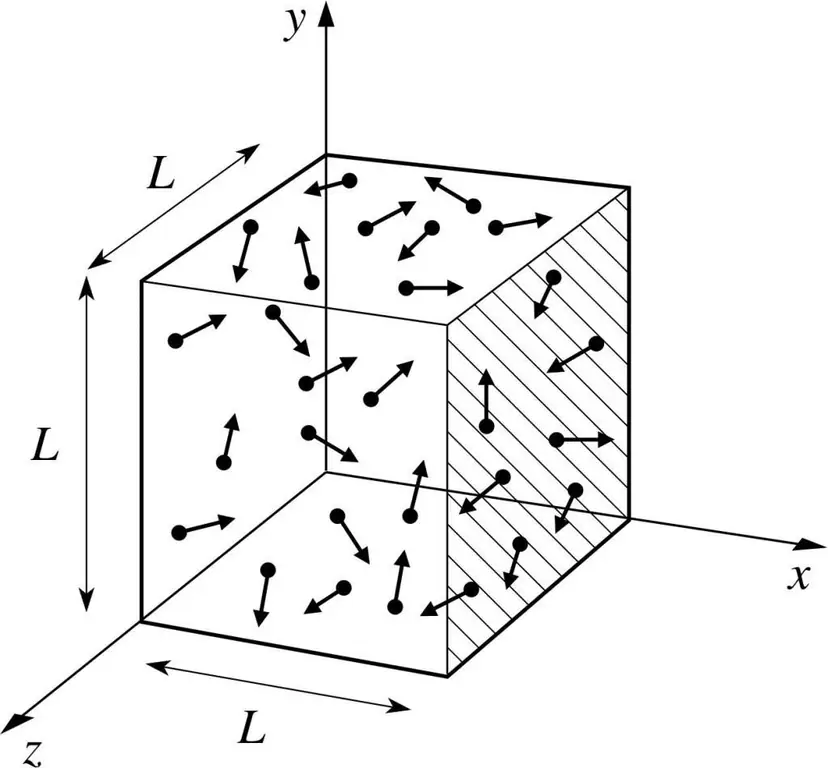
Hybnosť prebiehajúcej zrážky, ako vieme, je určená vzorcom: p=mv, ale v tomto prípade bude mať tento vzorec tvar projekcie: p=mv(x).
Keďže berieme do úvahy iba rozmer osi x, teda osi x, celkovú zmenu hybnosti vyjadríme vzorcom: mv(x) - m(-v(x))=2mv(x).
Ďalej zvážte silu, ktorou pôsobí náš objekt pomocou druhého Newtonovho zákona: F=ma=P/t.
Z týchto vzorcov vyjadríme tlak zo strany plynu: P=F/a;
Teraz dosadíme silový výraz do výsledného vzorca a získame: P=mv(x)^2/L^3.
Potom môže byť náš hotový tlakový vzorec napísaný pre N-tý počet molekúl plynu. Inými slovami, bude to vyzerať takto:
P=Nmv(x)^2/V, kde v je rýchlosť a V je objem.
Pokúsme sa teraz zdôrazniť niekoľko základných ustanovení o tlaku plynu:
- Prejavuje sa prostredníctvomzrážky molekúl s molekulami stien objektu, v ktorom sa nachádza.
- Veľkosť tlaku je priamo úmerná sile a rýchlosti dopadu molekúl na steny nádoby.
Niekoľko stručných záverov o teórii
Skôr než pôjdeme ďalej a zvážime základnú rovnicu molekulárnej kinetickej teórie, ponúkame vám niekoľko stručných záverov z vyššie uvedených bodov a teórie:
- Miera priemernej energie pohybu jej atómov a molekúl je absolútna teplota.
- Keď majú dva rôzne plyny rovnakú teplotu, ich molekuly majú rovnakú priemernú kinetickú energiu.
- Energia častíc plynu je priamo úmerná strednej štvorcovej rýchlosti: E=1/2mv^2.
- Hoci molekuly plynu majú priemernú kinetickú energiu a priemernú rýchlosť, jednotlivé častice sa pohybujú rôznymi rýchlosťami: niektoré rýchlo, niektoré pomaly.
- Čím vyššia teplota, tým vyššia rýchlosť molekúl.
- Koľkokrát zvýšime teplotu plynu (napríklad dvojnásobne), toľkokrát sa zvýši aj energia pohybu jeho častíc (resp. zdvojnásobí).
Základná rovnica a vzorce

Základná rovnica molekulárnej kinetickej teórie vám umožňuje stanoviť vzťah medzi veličinami mikrosveta a podľa toho aj makroskopickými, teda meranými veličinami.
Jeden z najjednoduchších modelov, ktoré môže molekulárna teória považovať za model ideálneho plynu.
Dalo by sa to tak povedaťtoto je druh imaginárneho modelu študovaného molekulárnou kinetickou teóriou ideálneho plynu, v ktorom:
- najjednoduchšie plynové častice sa považujú za dokonale elastické guľôčky, ktoré interagujú navzájom aj s molekulami stien akejkoľvek nádoby iba v jednom prípade - absolútne elastická zrážka;
- príťažlivé sily vo vnútri plynu chýbajú alebo ich možno v skutočnosti zanedbať;
- prvky vnútornej štruktúry plynu možno považovať za hmotné body, to znamená, že ich objem možno tiež zanedbať.
Fyzik nemeckého pôvodu Rudolf Clausius vzhľadom na takýto model napísal vzorec pre tlak plynu prostredníctvom vzťahu mikroskopických a makroskopických parametrov. Vyzerá to takto:
p=1/3m(0)nv^2.
Tento vzorec bude neskôr nazývaný ako základná rovnica molekulárno-kinetickej teórie ideálneho plynu. Môže byť prezentovaný v niekoľkých rôznych formách. Našou povinnosťou je teraz ukázať sekcie ako molekulárna fyzika, molekulárna kinetická teória, a teda ich kompletné rovnice a typy. Preto má zmysel zvážiť ďalšie variácie základného vzorca.
Vieme, že priemernú energiu charakterizujúcu pohyb molekúl plynu možno nájsť pomocou vzorca: E=m(0)v^2/2.
V tomto prípade môžeme nahradiť výraz m(0)v^2 v pôvodnom tlakovom vzorci priemernou kinetickou energiou. V dôsledku toho budeme mať možnosť zostaviť základnú rovnicu molekulárnej kinetickej teórie plynov v nasledujúcom tvare: p=2/3nE.
Okrem toho všetci vieme, že výraz m(0)n možno zapísať ako súčin dvoch kvocientov:
m/NN/V=m/V=ρ.
Po týchto manipuláciách môžeme prepísať náš vzorec pre rovnicu molekulárno-kinetickej teórie ideálneho plynu v tretej, inej forme:
p=1/3ρv^2.
No, to je možno všetko, čo potrebujete vedieť o tejto téme. Zostáva len systematizovať získané poznatky vo forme krátkych (a nie tak) záverov.
Všetky všeobecné závery a vzorce na tému "Molekulárno-kinetická teória"
Tak začnime.
Prvé:
Fyzika je základná veda zahrnutá do kurzu prírodných vied, ktorá študuje vlastnosti hmoty a energie, ich štruktúru, vzorce anorganickej prírody.
Zahŕňa nasledujúce sekcie:
- mechanika (kinematika a dynamika);
- static;
- termodynamika;
- elektrodynamika;
- molekulárna sekcia;
- optika;
- fyzika kvánt a atómového jadra.
Druhé:
Fyzika častíc a termodynamika sú úzko súvisiace odbory, ktoré študujú výlučne makroskopickú zložku celkového počtu fyzikálnych systémov, teda systémy pozostávajúce z obrovského počtu elementárnych častíc.
Sú založené na molekulárnej kinetickej teórii.
Tretí:
Jadrom veci je toto. Molekulárna kinetická teória podrobne popisuje štruktúru látky (častejšie štruktúru plynov ako pevných látok).a tekuté telá), založené na troch základných predpokladoch, ktoré boli zozbierané z predpokladov významných vedcov. Medzi nimi: Robert Hooke, Isaac Newton, Daniel Bernoulli, Michail Lomonosov a mnohí ďalší.
Štvrtý:
Tri základné princípy molekulárnej kinetickej teórie:
- Všetky látky (bez ohľadu na to, či sú kvapalné, pevné alebo plynné) majú zložitú štruktúru pozostávajúcu z menších častíc: molekúl a atómov.
- Všetky tieto jednoduché častice sú v nepretržitom chaotickom pohybe. Príklad: Brownov pohyb a difúzia.
- Všetky molekuly za akýchkoľvek podmienok vzájomne interagujú určitými silami, ktoré majú elektrický kameň.
Každé z týchto ustanovení molekulárnej kinetickej teórie je pevným základom pri štúdiu štruktúry hmoty.
Piaty:
Niekoľko hlavných bodov molekulárnej teórie pre model plynu:
- Všetky plyny sú tvorené elementárnymi časticami, ktoré nemajú určitú veľkosť, ale majú určitú hmotnosť. Inými slovami, objem týchto častíc je minimálny v porovnaní so vzdialenosťou medzi nimi.
- Atómy a molekuly plynov nemajú prakticky žiadnu potenciálnu energiu, respektíve ich celková energia sa rovná kinetickej.
- S touto pozíciou sme sa už zoznámili skôr - Brownov pohyb. To znamená, že častice plynu sú vždy v nepretržitom a náhodnom pohybe.
- Absolútne všetky vzájomné zrážky atómov a molekúl plynov sprevádzané posolstvom rýchlosti a energie sú úplne elastické. Toto jeznamená, že počas kolízie nedochádza k strate energie ani prudkým skokom v ich kinetickej energii.
- Za normálnych podmienok a konštantnej teploty je priemerná kinetická energia takmer všetkých plynov rovnaká.
Šiesty:
Závery z teórie o plynoch:
- Absolútna teplota je mierou priemernej kinetickej energie jej atómov a molekúl.
- Keď majú dva rôzne plyny rovnakú teplotu, ich molekuly majú rovnakú priemernú kinetickú energiu.
- Priemerná kinetická energia častíc plynu je priamo úmerná strednej kvadratickej rýchlosti: E=1/2mv^2.
- Hoci molekuly plynu majú priemernú kinetickú energiu a priemernú rýchlosť, jednotlivé častice sa pohybujú rôznymi rýchlosťami: niektoré rýchlo, niektoré pomaly.
- Čím vyššia teplota, tým vyššia rýchlosť molekúl.
- Koľkokrát zvýšime teplotu plynu (napríklad dvojnásobne), toľkokrát sa zvýši aj priemerná kinetická energia jeho častíc (resp. zdvojnásobí).
- Vzťah medzi tlakom plynu na steny nádoby, v ktorej sa nachádza, a intenzitou dopadov molekúl na tieto steny je priamo úmerný: čím viac nárazov, tým vyšší tlak a naopak.
Siedma:
Ideálny model plynu je model, v ktorom musia byť splnené nasledujúce podmienky:
- Molekuly plynu môžu a sú považované za dokonale elastické gule.
- Tieto loptičky môžu interagovať medzi sebou a so stenami ktorejkoľvek z nichplavidlo len v jednom prípade - absolútne elastická kolízia.
- Sily, ktoré popisujú vzájomný ťah medzi atómami a molekulami plynu, chýbajú alebo ich možno v skutočnosti zanedbať.
- Atómy a molekuly sa považujú za hmotné body, to znamená, že ich objem možno tiež zanedbať.
Ôsmy:
Poďme uviesť všetky základné rovnice a ukázať vzorce v téme "Molekulárno-kinetická teória":
p=1/3m(0)nv^2 - základná rovnica pre model ideálneho plynu odvodená nemeckým fyzikom Rudolfom Clausiusom.
p=2/3nE - základná rovnica molekulárno-kinetickej teórie ideálneho plynu. Odvodené z priemernej kinetickej energie molekúl.
р=1/3ρv^2 - rovnaká rovnica, ale uvažovaná prostredníctvom hustoty a strednej kvadratickej rýchlosti molekúl ideálneho plynu.
m(0)=M/N(a) - vzorec na nájdenie hmotnosti jednej molekuly prostredníctvom Avogadrovho čísla.
v^2=(v(1)+v(2)+v(3)+…)/N - vzorec na zistenie strednej štvorcovej rýchlosti molekúl, kde v(1), v(2), v (3) a tak ďalej - rýchlosť prvej molekuly, druhej, tretej a tak ďalej až po n-tú molekulu.
n=N/V - vzorec na zistenie koncentrácie molekúl, kde N je počet molekúl v objeme plynu k danému objemu V.
E=mv^2/2=3/2kT - vzorce na zistenie priemernej kinetickej energie molekúl, kde v^2 je stredná odmocnina kvadratickej rýchlosti molekúl, k je konštanta hodnota pomenovaná po rakúskej fyzike Ludwiga Boltzmanna a T je teplota plynu.
p=nkT - tlakový vzorec z hľadiska koncentrácie, konštantnýBoltzmann a absolútna teplota T. Z toho vyplýva ďalší základný vzorec, ktorý objavili ruský vedec Mendelejev a francúzsky fyzik-inžinier Claiperon:
pV=m/MRT, kde R=kN(a) je univerzálna konštanta pre plyny.
Teraz ukážme konštanty pre rôzne izoprocesy: izobarické, izochorické, izotermické a adiabatické.
pV/T=const - vykonáva sa, keď je hmotnosť a zloženie plynu konštantné.
рV=konst - ak je konštantná aj teplota.
V/T=const - ak je tlak plynu konštantný.
p/T=const - ak je objem konštantný.
To je možno všetko, čo potrebujete vedieť o tejto téme.
Dnes sme sa vrhli do takej vedeckej oblasti, akou je teoretická fyzika, jej viaceré sekcie a bloky. Podrobnejšie sme sa dotkli takej oblasti fyziky, ako je základná molekulová fyzika a termodynamika, konkrétne molekulárno-kinetická teória, ktorá, ako sa zdá, nepredstavuje žiadne ťažkosti v počiatočnej štúdii, ale v skutočnosti má veľa úskalí.. Rozširuje naše chápanie modelu ideálneho plynu, ktorý sme tiež podrobne študovali. Okrem toho stojí za zmienku, že sme sa oboznámili aj so základnými rovnicami molekulárnej teórie v ich rôznych obmenách a zvážili sme aj všetky najpotrebnejšie vzorce na nájdenie určitých neznámych veličín na túto tému, čo bude užitočné najmä pri príprave na písanie akékoľvek testy, skúšky a testy, prípadne na rozšírenie všeobecného rozhľadu a vedomostí z fyziky.
Dúfame, že tento článok bol pre vás užitočný a vytiahli ste z neho len tie najnutnejšie informácie, ktoré posilňujú vaše znalosti v takých pilieroch termodynamiky, ako sú základné ustanovenia molekulárnej kinetickej teórie.






