Ako viete, každá fyzikálna veličina patrí do jedného z dvoch typov, je buď skalárna alebo vektorová. V tomto článku zvážime také kinematické charakteristiky, ako je rýchlosť a zrýchlenie, a tiež ukážeme, kam smerujú vektory zrýchlenia a rýchlosti.
Čo je rýchlosť a zrýchlenie?
Obe veličiny uvedené v tomto odseku sú dôležitými charakteristikami akéhokoľvek druhu pohybu, či už ide o pohyb tela v priamke alebo po zakrivenej dráhe.
Rýchlosť je rýchlosť, ktorou sa súradnice menia v priebehu času. Matematicky sa táto hodnota rovná časovej derivácii prejdenej vzdialenosti, teda:
v¯=dl¯/dt.
Vektor l¯ je nasmerovaný z počiatočného bodu cesty do koncového bodu.
Zrýchlenie je zase rýchlosť, s ktorou sa samotná rýchlosť mení v čase. Vo forme vzorca ho možno napísať takto:
a¯=dv¯/dt.
Samozrejme, ak vezmeme druhú deriváciu zvektor posunutia l¯ v čase, dostaneme aj hodnotu zrýchlenia.
Keďže rýchlosť sa meria v metroch za sekundu, zrýchlenie sa podľa písomného vyjadrenia meria v metroch za sekundu na druhú.

Kde sú vektory zrýchlenia a rýchlosti?
Vo fyzike je každý mechanický pohyb telesa zvyčajne charakterizovaný určitou trajektóriou. Tá posledná je nejaká imaginárna krivka, po ktorej sa teleso pohybuje v priestore. Napríklad priama čiara alebo kruh sú hlavnými príkladmi bežných dráh pohybu.
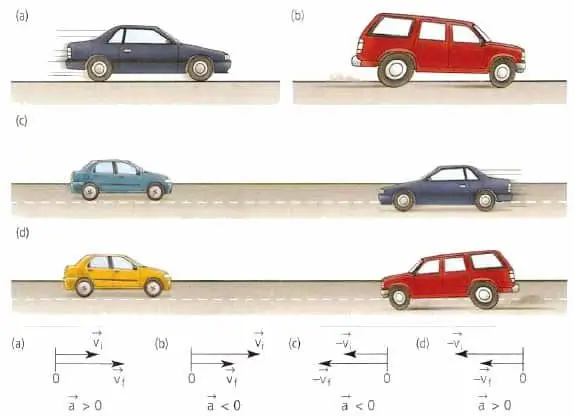
Vektor rýchlosti tela je vždy nasmerovaný v smere pohybu, bez ohľadu na to, či sa teleso spomaľuje alebo zrýchľuje, či sa pohybuje po priamke alebo po krivke. V geometrických podmienkach je vektor rýchlosti nasmerovaný tangenciálne k bodu trajektórie, v ktorej sa teleso momentálne nachádza.
Vektor zrýchlenia materiálu alebo bodu tela nemá nič spoločné s rýchlosťou. Tento vektor je nasmerovaný v smere zmeny rýchlosti. Napríklad pre priamočiary pohyb sa hodnota a¯ môže zhodovať v smere s v¯ alebo byť opačná k v¯.
Sila pôsobiaca na telo a zrýchlenie
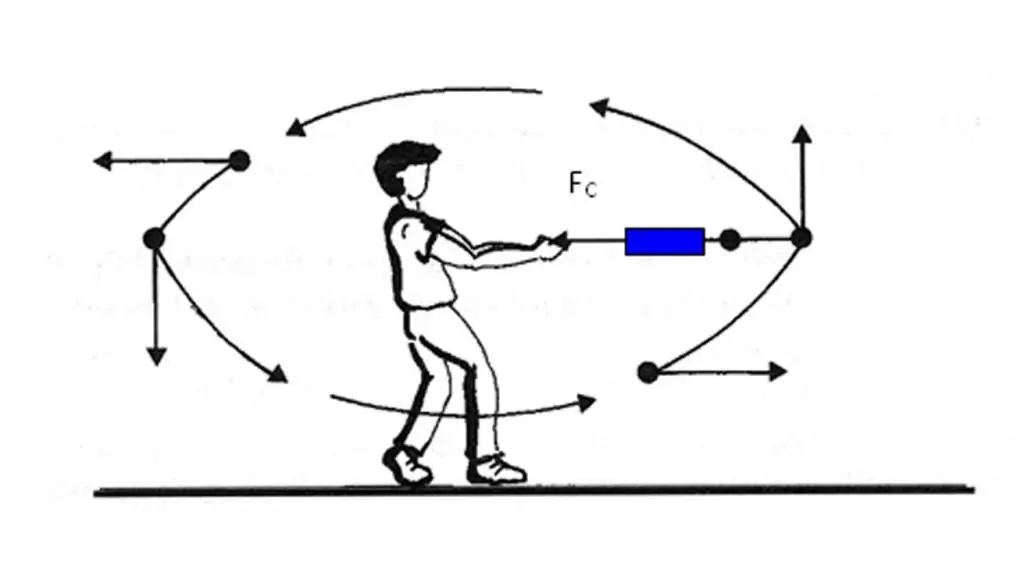
Zistili sme, že vektor zrýchlenia telesa smeruje k zmene vektora rýchlosti. Nie je však vždy jednoduché určiť, ako sa mení rýchlosť v danom bode trajektórie. Okrem toho na určenie zmeny rýchlosti je potrebné vykonať operáciuvektorové rozdiely. Aby ste sa vyhli týmto ťažkostiam pri určovaní smeru vektora a¯, existuje iný spôsob, ako to rýchlo zistiť.
Nižšie je Newtonov slávny a dobre známy zákon každému študentovi:
F¯=ma¯.
Vzorec ukazuje, že príčinou zrýchlenia v telesách je sila, ktorá na ne pôsobí. Keďže hmotnosť m je skalárna, vektor sily F¯ a vektor zrýchlenia a¯ sú v rovnakom smere. Na túto skutočnosť treba pamätať a aplikovať ju v praxi vždy, keď je potrebné určiť smer veličiny a¯.
Ak na teleso pôsobí niekoľko rôznych síl, potom sa smer vektora zrýchlenia bude rovnať výslednému vektoru všetkých síl.
Kruhový pohyb a zrýchlenie
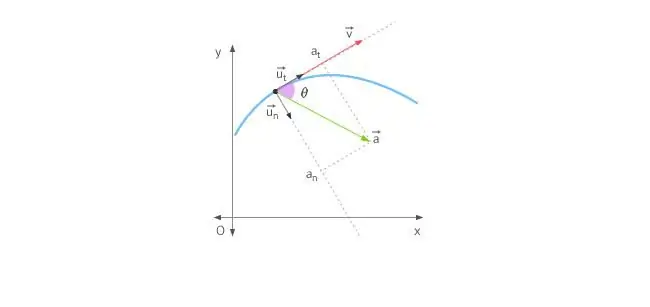
Keď sa teleso pohybuje v priamom smere, zrýchlenie smeruje dopredu alebo dozadu. V prípade pohybu po kružnici je situácia komplikovaná tým, že vektor rýchlosti neustále mení svoj smer. Vzhľadom na vyššie uvedené je celkové zrýchlenie určené jeho dvoma zložkami: tangenciálnym a normálnym zrýchlením.
Tangenciálne zrýchlenie smeruje presne rovnako ako vektor rýchlosti alebo proti nemu. Inými slovami, táto zložka zrýchlenia smeruje pozdĺž dotyčnice k trajektórii. Tangenciálne zrýchlenie popisuje zmenu modulu samotnej rýchlosti.
Normálne zrýchlenie smeruje pozdĺž normály k danému bodu trajektórie, pričom sa berie do úvahy jej zakrivenie. V prípade kruhového pohybu udáva vektor tejto zložkydo stredu, to znamená, že normálne zrýchlenie smeruje pozdĺž polomeru otáčania. Tento komponent sa často nazýva dostredivý.
Úplné zrýchlenie je súčet týchto zložiek, takže jeho vektor môže byť nasmerovaný ľubovoľne vzhľadom na kružnicu.
Ak sa teleso otáča bez zmeny lineárnej rýchlosti, potom existuje iba nenulová normálna zložka, takže vektor plného zrýchlenia smeruje do stredu kruhu. Všimnite si, že toto centrum je tiež ovplyvnené silou, ktorá udržuje telo na jeho trajektórii. Napríklad gravitačná sila Slnka udržuje našu Zem a ostatné planéty na ich obežných dráhach.






