Jednou z hlavných úloh analýzy dynamických riadiacich systémov je riešenie problému ich stability. Ich stabilita je jednou z najdôležitejších charakteristík koncepcie riadenia. Systém sa považuje za nestabilný, ak sa nevráti do svojej pôvodnej polohy, ale naďalej osciluje po tom, čo prejde určitými zmenami na vstupe, alebo je pod vplyvom nežiaducich porúch.
Definícia hlavného konceptu
Podľa koncepcie stability systému je stav jeho rovnováhy spôsobený absenciou vplyvu rušivých faktorov na systém. V tejto situácii má rozdiel medzi nastaveným a skutočným stavom tendenciu k nule. Stabilita je schopnosť vrátiť sa do pôvodného rovnovážneho stavu po tom, čo sa skončí porucha, ktorá viedla k jej porušeniu. Nestabilný systém sa vplyvom poruchy vzďaľuje od rovnovážneho stavu alebo osciluje, pričom amplitúda postupnestúpa.

Podmienky stability
Pre stabilitu systému s konštantným časom musia byť splnené tieto dve podmienky:
- Vytvorí obmedzený výstup pre každý vstup; ak neexistuje žiadny vstup, výstup musí byť nula, bez ohľadu na akékoľvek počiatočné podmienky.
- Stabilitu systému možno nazvať absolútnou alebo relatívnou stabilitou. Uvedený pojem sa používa v súvislosti so štúdiou, v ktorej sa porovnávajú určité veličiny, ich prevádzkové podmienky. Stabilita je konečný výsledok vytvorený výsledkom.
Ak je výstup systému nekonečný, aj keď je naň aplikovaný konečný vstup, potom sa bude hovoriť, že je nestabilný, t. j. inherentne stabilný, má ohraničené ukončenie, keď sa naň aplikuje ohraničený začiatok sám.
Vstupom sa v tomto prípade rozumejú rôzne body aplikácie vplyvu vonkajšieho prostredia na systém. Výstupom je konečný produkt jej činnosti, ktorý má formu transformovaných vstupných dát.
V spojitom lineárnom časovom systéme je možné zapísať podmienku stability pre konkrétnu impulznú odozvu.
Keď je diskrétny, index stability možno zapísať aj pre konkrétnu impulznú odozvu.
Pre nestabilnú podmienku v spojitých aj ohraničených systémoch budú tieto výrazy nekonečné.
Typy stability a rušenia
StatickýStabilita systému je chápaná ako jeho schopnosť zabezpečiť obnovenie pôvodného (alebo pôvodného) režimu po malej poruche. Pod pojmom prezentovaným v tejto súvislosti uvažujú o výkyvoch, ktoré ovplyvňujú jeho správanie bez ohľadu na to, kde sa skok alebo pokles objaví a aká je ich veľkosť. Na základe toho nám tieto režimy, ktoré sú blízke pôvodnému, umožňujú považovať ho za lineárny.
Dynamická stabilita systémov je schopnosť systémov obnoviť počiatočný stav po veľkej poruche.
Pod veľkým kolísaním sa rozumie taký pohyb, ktorého povaha vplyvu a jeho zodpovedajúce správanie určuje dobu existencie, veľkosť a miesto jeho vzniku.
Na základe toho je systém v tomto rozsahu definovaný ako nelineárny.
Kritériá na určenie udržateľnosti
Hlavnou podmienkou stability lineárneho systému nie je povaha poruchy, ale jej štruktúra. Predpokladá sa, že táto stabilita „v malom“je určená, ak nie sú stanovené jej hranice. Stabilita „vo veľkom“je určená limitmi a zhodou skutočných odchýlok s týmito stanovenými limitmi.
Na určenie stability systému sa používajú nasledujúce kritériá:
- koreňové kritérium;
- Stodolské kritérium;
- Hurwitzovo kritérium;
- Nyquistovo kritérium;
- Michajlovovo kritérium a ďalšie
Na určenie stability jednotlivých odkazov sa používa koreňové kritérium a Stodolova vyhodnocovacia technikaa otvorené systémy. Hurwitzovo kritérium je algebraické a umožňuje určiť stabilitu uzavretých systémov bez oneskorenia. Kritériá Nyquist a Michajlov sú frekvenčné. Používajú sa na určenie stability uzavretých systémov na základe ich frekvenčnej odozvy.

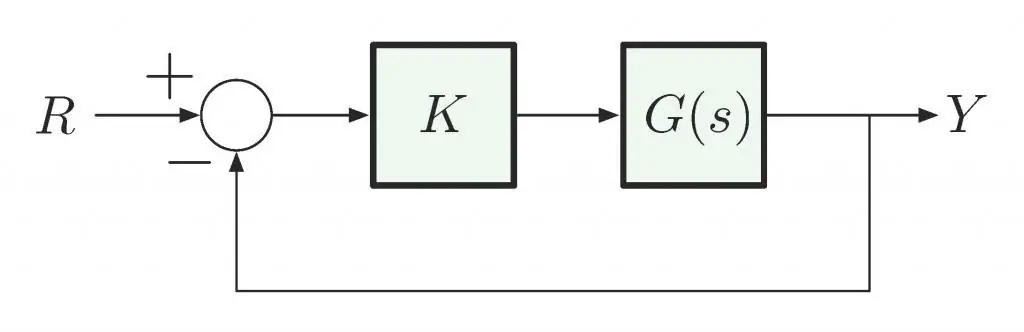
Základné kritérium
Umožňuje určiť stabilitu systému na základe formy prenosovej funkcie. Jeho vlastnosti správania sú opísané charakteristickým polynómom (menovateľom prenosovej funkcie). Ak priradíme menovateľa k nule, korene výslednej rovnice nám umožnia určiť stupeň stability.
Podľa tohto kritéria bude lineárny systém stabilný, ak všetky korene rovnice budú v ľavej polrovine. Ak sa aspoň jeden z nich nachádza na hranici stability, bude tiež na hranici. Ak je aspoň jeden z nich v pravej polrovine, systém možno považovať za nestabilný.
Stodola Criterion
Vyplýva to z koreňovej definície. V súlade so Stodolovým kritériom možno lineárny systém považovať za stabilný, ak sú všetky koeficienty polynómu kladné.
Hurwitzovo kritérium
Toto kritérium sa používa pre charakteristický polynóm uzavretého systému. Podľa tejto techniky je dostatočnou podmienkou stability skutočnosť, že hodnota determinantu a všetkých hlavných diagonálnych minorov matice je väčšia ako nula. Ak je aspoň jeden z nich rovnakýnula, uvažuje sa na hranici stability. Ak existuje aspoň jeden negatívny determinant, mal by sa považovať za nestabilný.
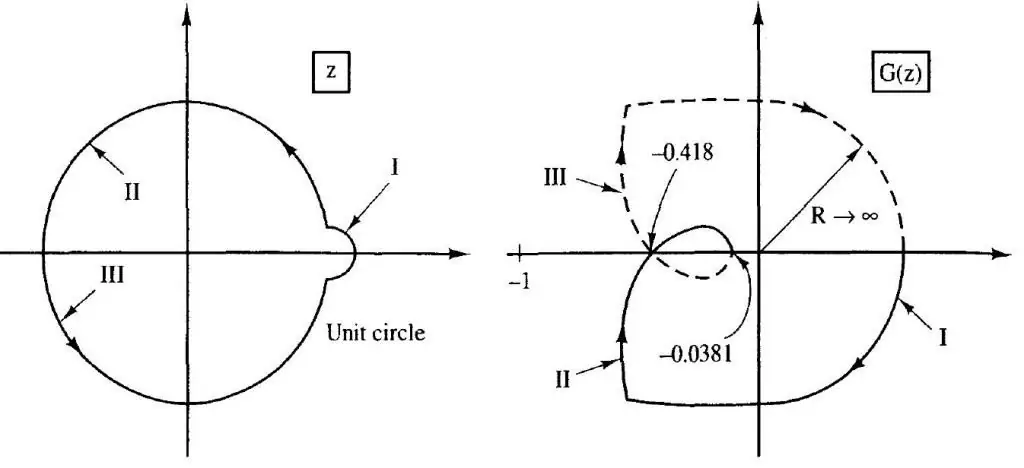
Nyquistovo kritérium
Základom tejto techniky je konštrukcia krivky spájajúcej konce vektora premennej, ktorá zobrazuje prenosovú funkciu. Formulácia kritéria je nasledovná: uzavretý systém sa považuje za stabilný, ak funkčná krivka neohraničuje bod so súradnicami (-1, j0) v komplexnej rovine.
Systém finančnej spoľahlivosti
Finančná odolnosť je stav, v ktorom je systém, t. j. kľúčové trhy a inštitúcie, odolný voči ekonomickým otrasom a pripravený hladko vykonávať svoje základné funkcie, ako je sprostredkovanie peňažných tokov, riadenie rizík a platobné opatrenia.
Vzhľadom na vzájomnú závislosť poskytovania tlmočenia (vertikálne aj horizontálne) musí analýza pokrývať celý systém finančného sprostredkovania. Inými slovami, okrem bankového sektora je potrebné analyzovať aj nebankové inštitúcie, ktoré sa v tej či onej forme zaoberajú sprostredkovaním. Patria sem mnohé typy inštitúcií vrátane maklérskych firiem, investičných fondov, poisťovateľov a iných (rôznych) subjektov. Pri analýze systému finančnej stability sa skúma miera, do akej je celá štruktúra schopná odolávať vonkajším a vnútorným šokom. Samozrejme, nie vždy ku krízam vedú otrasy, ale samotné nestabilné finančné prostrediesám o sebe môže brániť zdravému rozvoju ekonomiky.
Rôzne teórie identifikujú príčiny finančnej nestability. Ich relevantnosť sa môže líšiť v závislosti od obdobia a krajín zapojených do rozsahu analýzy. Medzi problematické faktory, ktoré ovplyvňujú celý finančný systém, literatúra zvyčajne označuje nasledovné:
- rýchla liberalizácia finančného sektora;
- neprimeraná hospodárska politika;
- Mechanizmus necieleného výmenného kurzu;
- neefektívne prideľovanie zdrojov;
- slabý dozor;
- Neprimeraná regulácia účtovníctva a auditu.
Možné príčiny sa objavujú nielen hromadne, ale aj jednotlivo alebo v náhodnej kombinácii, preto je analýza finančnej stability mimoriadne náročná úloha. Zameranie sa na jednotlivé odvetvia skresľuje celkový obraz, takže v priebehu štúdia finančnej stability je potrebné tieto problémy posudzovať v ich komplexnosti.

Proces analýzy stability podnikového systému prebieha v niekoľkých fázach.
Na začiatku sa vyhodnocujú a analyzujú absolútne a relatívne ukazovatele finančnej stability. V druhej fáze sú faktory rozdelené podľa ich významnosti, kvalitatívne a kvantitatívne sa hodnotí ich vplyv.
Pomery finančnej sily podnikov
Finančná situácia spoločnosti, jej stabilita do značnej miery závisí od optimálnej štruktúry zdrojov kapitálu, teda pomeru dlhu k vlastným zdrojom, od optimálnejštruktúre majetku spoločnosti a predovšetkým na pomere stálych a obežných aktív, ako aj stavu prostriedkov a pasív spoločnosti.
Preto je dôležité preštudovať si štruktúru zdrojov rizikového kapitálu a posúdiť mieru finančnej stability a rizika. Na tento účel sa používajú koeficienty stability systému:
- koeficient autonómie (nezávislosti) - podiel kapitálu v súvahe;
- pomer závislosti - podiel vypožičaného kapitálu v súvahe;
- aktuálny dlhový pomer - pomer krátkodobých finančných záväzkov k súvahe;
- pomer finančnej stability (dlhodobá finančná nezávislosť) - pomer kapitálu a dlhodobého dlhu k súvahe;
- pomer krytia dlhu (ukazovateľ solventnosti) - pomer kapitálu k dlhu;
- pomer finančnej páky (pomer finančného rizika) - pomer dlhu ku kapitálu.

Čím vyššia je úroveň ukazovateľov ako autonómia, finančná stabilita, krytie dlhového kapitálu, tým nižšia je úroveň ďalšej skupiny koeficientov (závislosť, aktuálny dlh, dlhodobé záväzky voči investorom) a teda aj stabilita finančnej situácie spoločnosti. Finančná páka sa tiež nazýva finančná páka.






