Štúdium procesov prebiehajúcich v štatistických systémoch komplikuje minimálna veľkosť častíc a ich obrovský počet. Je prakticky nemožné posudzovať každú časticu samostatne, preto sa zavádzajú štatistické veličiny: priemerná rýchlosť častíc, ich koncentrácia, hmotnosť častíc. Vzorec, ktorý charakterizuje stav systému, berúc do úvahy mikroskopické parametre, sa nazýva základná rovnica molekulárno-kinetickej teórie plynov (MKT).
Niečo o priemernej rýchlosti častíc
Stanovenie rýchlosti častíc bolo najskôr uskutočnené experimentálne. Známy experiment zo školských osnov, ktorý viedol Otto Stern, umožnil vytvoriť predstavu o rýchlostiach častíc. Počas experimentu sa študoval pohyb atómov striebra v rotujúcich valcoch: najprv v stacionárnom stave zariadenia, potom keď sa otáčalo určitou uhlovou rýchlosťou.
V dôsledku toho sa zistilo, že rýchlosť molekúl striebra prevyšuje rýchlosť zvuku a je 500 m/s. Skutočnosť je celkom zaujímavá, pretože pre človeka je ťažké cítiť také rýchlosti pohybu častíc v látkach.
Ideálny plyn
Pokračovať vo výskumeZdá sa, že je to možné len v systéme, ktorého parametre možno určiť priamym meraním pomocou fyzikálnych prístrojov. Rýchlosť sa meria rýchlomerom, ale myšlienka pripojenia rýchlomera k jednej častici je absurdná. Priamo možno merať iba makroskopický parameter spojený s pohybom častíc.
Zvážte tlak plynu. Tlak na steny nádoby vzniká nárazmi molekúl plynu v nádobe. Zvláštnosťou plynného stavu hmoty je dostatočne veľká vzdialenosť medzi časticami a ich malá vzájomná interakcia. To vám umožňuje priamo merať jeho tlak.
Akýkoľvek systém interagujúcich telies je charakterizovaný potenciálnou energiou a kinetickou energiou pohybu. Skutočný plyn je zložitý systém. Variabilita potenciálnej energie nie je vhodná na systematizáciu. Problém sa dá vyriešiť zavedením modelu, ktorý nesie charakteristické vlastnosti plynu, čím sa zloží zložitosť interakcie.
Ideálny plyn je stav hmoty, v ktorom je interakcia častíc zanedbateľná, potenciálna energia interakcie má tendenciu k nule. Za významnú možno považovať iba energiu pohybu, ktorá závisí od rýchlosti častíc.
Ideálny tlak plynu
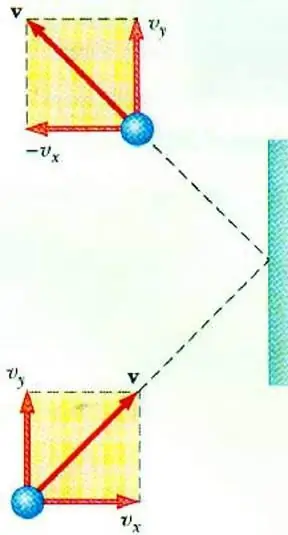
Odhaliť vzťah medzi tlakom plynu a rýchlosťou jeho častíc umožňuje základná rovnica MKT ideálneho plynu. Častica pohybujúca sa v nádobe pri náraze na stenu prenáša na ňu impulz, ktorého hodnotu možno určiť na základe druhého zákonaNewton:
F∆t=2 m0vx
Zmena hybnosti častice počas elastického nárazu je spojená so zmenou horizontálnej zložky jej rýchlosti. F je sila pôsobiaca zo strany častice na stenu po krátky čas t; m0 - hmotnosť častíc.
Všetky častice plynu narážajú na povrch plochy S počas času ∆t, pohybujú sa v smere k povrchu rýchlosťou vx a nachádzajú sa vo valci objemu Sυ x Δt. Pri koncentrácii častíc n sa presne polovica molekúl pohybuje smerom k stene, druhá polovica sa pohybuje v opačnom smere.
Po zvážení zrážky všetkých častíc môžeme napísať Newtonov zákon pre silu pôsobiacu na plochu:
F∆t=nm0vx2S∆t
Keďže tlak plynu je definovaný ako pomer sily pôsobiacej kolmo na povrch k ploche povrchu, môžeme napísať:
p=F: S=nm0vx2
Výsledný vzťah ako základná rovnica MKT nemôže opísať celý systém, pretože sa uvažuje iba o jednom smere pohybu.
distribúcia Maxwell
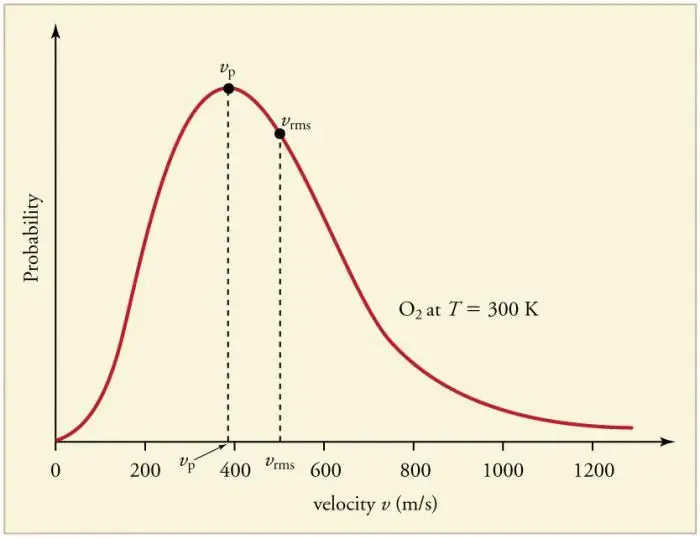
Nepretržité časté kolízie častíc plynu so stenami a medzi sebou navzájom vedú k vytvoreniu určitého štatistického rozloženia častíc z hľadiska rýchlostí (energií). Smery všetkých vektorov rýchlosti sa ukážu ako rovnako pravdepodobné. Toto rozdelenie sa nazýva Maxwellovo rozdelenie. V roku 1860 bol tento vzorodvodil J. Maxwell na základe MKT. Hlavné parametre distribučného zákona sa nazývajú rýchlosti: pravdepodobná, zodpovedajúca maximálnej hodnote krivky, a odmocnina vkv=√‹v2 › - stredná druhá mocnina rýchlosti častice.
Zvýšenie teploty plynu zodpovedá zvýšeniu rýchlosti.
Na základe skutočnosti, že všetky rýchlosti sú rovnaké a ich moduly majú rovnakú hodnotu, môžeme predpokladať:
‹v2›=‹vx2› + ‹v y2› + ‹vz2›, od: ‹ vx2›=‹v2›: 3
Základná rovnica MKT, berúc do úvahy priemernú hodnotu tlaku plynu, je:
p=nm0‹v2›: 3.
Tento vzťah je jedinečný v tom, že určuje vzťah medzi mikroskopickými parametrami: rýchlosťou, hmotnosťou častíc, koncentráciou častíc a tlakom plynu vo všeobecnosti.
Pomocou konceptu kinetickej energie častíc možno základnú rovnicu MKT prepísať inak:
p=2nm0‹v2›: 6=2n‹Ek›: 3
Tlak plynu je úmerný priemernej hodnote kinetickej energie jeho častíc.
Teplota
Je zaujímavé, že pre konštantné množstvo plynu v uzavretej nádobe je možné dať do súvisu tlak plynu a priemernú hodnotu energie pohybu častíc. V tomto prípade je možné merať tlak meraním energiečastice.
Čo robiť? Akú hodnotu možno porovnať s kinetickou energiou? Teplota sa ukáže ako taká hodnota.

Teplota je miera tepelného stavu látok. Na jej meranie sa používa teplomer, ktorého základom je tepelná rozťažnosť pracovnej tekutiny (alkohol, ortuť) pri zahriatí. Stupnica teplomera je vytvorená experimentálne. Zvyčajne sú na ňom umiestnené značky zodpovedajúce polohe pracovnej tekutiny počas nejakého fyzikálneho procesu prebiehajúceho v konštantnom tepelnom stave (vriaca voda, topiaci sa ľad). Rôzne teplomery majú rôzne stupnice. Napríklad Celzia, Fahrenheita.

Univerzálna teplotná stupnica
Plynové teplomery možno považovať za zaujímavejšie z hľadiska nezávislosti od vlastností pracovnej tekutiny. Ich mierka nezávisí od druhu použitého plynu. V takomto zariadení je možné hypoteticky určiť teplotu, pri ktorej má tlak plynu tendenciu k nule. Výpočty ukazujú, že táto hodnota zodpovedá -273,15 oC. Teplotná stupnica (absolútna teplotná stupnica alebo Kelvinova stupnica) bola zavedená v roku 1848. Ako hlavný bod tejto stupnice bola braná možná teplota nulového tlaku plynu. Jednotkový segment stupnice sa rovná jednotkovej hodnote stupnice Celzia. Zdá sa pohodlnejšie zapísať si základnú rovnicu MKT pomocou teploty pri štúdiu procesov plynov.
Vzťah medzi tlakom a teplotou
Empiricky si to môžete overiťúmernosť tlaku plynu k jeho teplote. Zároveň sa zistilo, že tlak je priamo úmerný koncentrácii častíc:
P=nkT,
kde T je absolútna teplota, k je konštanta rovná 1,38•10-23J/K.
Základná hodnota, ktorá má konštantnú hodnotu pre všetky plyny, sa nazýva Boltzmannova konštanta.
Porovnaním závislosti tlaku od teploty a základnej rovnice plynov MKT môžeme napísať:
‹Ek›=3 kT: 2
Priemerná hodnota kinetickej energie pohybu molekúl plynu je úmerná jeho teplote. To znamená, že teplota môže slúžiť ako miera kinetickej energie pohybu častíc.






