Prírodné javy a procesy okolo nás sú pomerne zložité. Na ich presný fyzikálny popis treba použiť ťažkopádny matematický aparát a vziať do úvahy veľké množstvo významných faktorov. Aby sa predišlo tomuto problému, vo fyzike sa používajú niektoré zjednodušené modely, ktoré značne uľahčujú matematickú analýzu procesu, ale prakticky neovplyvňujú presnosť jeho popisu. Jedným z nich je model ideálneho plynu. Pozrime sa na to podrobnejšie v článku.
Koncept ideálneho plynu
Ideálny plyn je stav agregácie látky, ktorý pozostáva z hmotných bodov, ktoré spolu neinteragujú. Vysvetlime si túto definíciu podrobnejšie.
Po prvé, hovoríme o hmotných bodoch ako o objektoch, ktoré tvoria ideálny plyn. To znamená, že jeho molekuly a atómy nemajú veľkosť, ale majú určitú hmotnosť. Je to odvážnemožno urobiť aproximáciu s prihliadnutím na skutočnosť, že vo všetkých skutočných plynoch pri nízkych tlakoch a vysokých teplotách je vzdialenosť medzi molekulami oveľa väčšia ako ich lineárne rozmery.
Po druhé, molekuly v ideálnom plyne by spolu nemali interagovať. V skutočnosti takéto interakcie vždy existujú. Takže dokonca aj atómy vzácnych plynov zažívajú dipólovo-dipólovú príťažlivosť. Inými slovami, van der Waalsove interakcie sú prítomné. V porovnaní s kinetickou energiou rotácie a translačného pohybu molekúl sú však tieto interakcie také malé, že neovplyvňujú vlastnosti plynov. Preto ich nemožno brať do úvahy pri riešení praktických problémov.
Je dôležité poznamenať, že nie všetky plyny s nízkou hustotou a vysokou teplotou možno považovať za ideálne. Okrem van der Waalsových interakcií existujú aj iné, silnejšie typy väzieb, napríklad vodíkové väzby medzi molekulami H2O, ktoré vedú k hrubému porušeniu podmienok ideálnosti plynu. Z tohto dôvodu nie je ideálnym plynom vodná para, ale vzduch áno.
Fyzikálny model ideálneho plynu
Tento model možno znázorniť takto: predpokladajme, že plynový systém obsahuje N častíc. Môžu to byť atómy a molekuly rôznych chemikálií a prvkov. Počet N častíc je veľký, preto sa na jeho popis zvyčajne používa jednotka „mol“(1 mol zodpovedá Avogadrovmu číslu). Všetky sa pohybujú v určitom objeme V. Pohyby častícsú chaotické a navzájom nezávislé. Každý z nich má určitú rýchlosť v a pohybuje sa po priamej dráhe.
Teoreticky je pravdepodobnosť kolízie medzi časticami takmer nulová, pretože ich veľkosť je malá v porovnaní so vzdialenosťami medzi časticami. Ak však dôjde k takejto zrážke, potom je absolútne elastická. V druhom prípade sa zachová celková hybnosť častíc a ich kinetická energia.
Uvažovaný model ideálnych plynov je klasický systém s obrovským počtom prvkov. Preto sa rýchlosť a energia častíc v ňom riadi štatistickým rozložením Maxwell-Boltzmanna. Niektoré častice majú nízke rýchlosti, zatiaľ čo iné majú vysoké rýchlosti. V tomto prípade existuje určitý úzky rýchlostný limit, v ktorom ležia najpravdepodobnejšie hodnoty tejto veličiny. Rozdelenie rýchlosti molekúl dusíka je schematicky znázornené nižšie.
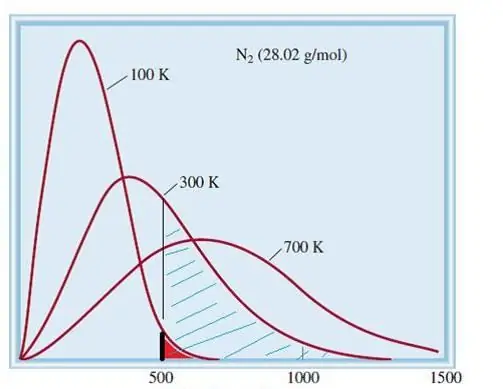
Kinetická teória plynov
Vyššie popísaný model ideálnych plynov jednoznačne určuje vlastnosti plynov. Tento model prvýkrát navrhol Daniel Bernoulli v roku 1738.

Následne ho do súčasného stavu vyvinuli August Kroenig, Rudolf Clausius, Michail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski a ďalší vedci.
Kinetická teória tekutých látok, na základe ktorej je zostavený model ideálneho plynu, vysvetľuje dve dôležité makroskopické vlastnosti systému založené na jeho mikroskopickom správaní:
- Tlak v plynoch je výsledkom kolízie častíc so stenami nádoby.
- Teplota v systéme je výsledkom prejavu neustáleho pohybu molekúl a atómov.
Rozvinieme oba závery kinetickej teórie.
Tlak plynu
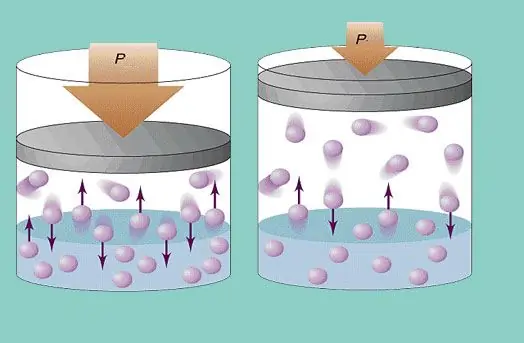
Model ideálneho plynu predpokladá neustály chaotický pohyb častíc v systéme a ich neustálu kolíziu so stenami nádoby. Každá takáto zrážka sa považuje za absolútne elastickú. Hmotnosť častíc je malá (≈10-27-10-25 kg). Preto pri kolízii nemôže vytvoriť veľký tlak. Napriek tomu je počet častíc a tým aj počet zrážok obrovský (≈1023). Okrem toho je stredná kvadratická rýchlosť prvkov pri izbovej teplote niekoľko stoviek metrov za sekundu. To všetko vedie k vytvoreniu značného tlaku na steny nádoby. Dá sa vypočítať pomocou nasledujúceho vzorca:
P=Nmvcp2 / (3V), kde vcp je stredná kvadratická rýchlosť, m je hmotnosť častice.
Absolútna teplota
Podľa modelu ideálneho plynu je teplota jednoznačne určená priemernou kinetickou energiou molekuly alebo atómu v skúmanom systéme. Môžete napísať nasledujúci výraz, ktorý súvisí s kinetickou energiou a absolútnou teplotou ideálneho plynu:
mvcp2 / 2=3 / 2kB T.
Tu kB je Boltzmannova konštanta. Z tejto rovnosti dostaneme:
T=m vcp2 / (3kB).
Univerzálna stavová rovnica
Ak spojíme vyššie uvedené výrazy pre absolútny tlak P a absolútnu teplotu T, môžeme napísať nasledujúcu rovnosť:
PV=nRT.
N je množstvo látky v móloch, R je plynová konštanta zavedená D. I. Mendelejevom. Tento výraz je najdôležitejšou rovnicou v teórii ideálnych plynov, pretože kombinuje tri termodynamické parametre (V, P, T) a nezávisí od chemických charakteristík plynového systému.

Univerzálnu rovnicu prvýkrát experimentálne odvodil francúzsky fyzik Emile Clapeyron v 19. storočí a potom ju do modernej podoby priniesol ruský chemik Mendelejev, a preto v súčasnosti nesie mená týchto vedcov.






