Pyramída spolu s hranolom je dokonalý mnohosten v trojrozmernom priestore, ich geometrické charakteristiky sa študujú na strednej škole. V tomto článku sa zamyslíme nad tým, čo sú pyramídy, z akých prvkov sa skladajú a tiež stručne charakterizujeme správne pyramídy.
Geometrická pyramída
Z hľadiska geometrie je pyramída priestorovým útvarom, ktorý pozostáva z jedného mnohouholníka a niekoľkých trojuholníkov. Získanie tohto čísla je celkom jednoduché. Aby ste to urobili, zoberte mnohouholník s n stranami, potom vyberte ľubovoľný bod v priestore, ktorý nebude ležať v rovine mnohouholníka, a pripojte každý vrchol mnohouholníka k tomuto bodu. Je zrejmé, že takto vytvorený obrazec bude mať n trojuholníkov spojených navzájom v jednom vrchole.
Pre vizualizáciu geometrického tvaru opísanej figúry si urobme obrázok.

Toto zobrazuje štvorhrannú pyramídu, ktorej základňa ještvoruholník a bočnú plochu tvoria štyri trojuholníky, ktoré majú spoločný vrchol.
Prvky pyramídy
Ako každý mnohosten, aj pyramídu tvoria tri typy prvkov:
- edges;
- tops;
- rebierka.
Tváre sú časti rovín, ktoré oddeľujú vnútorný objem postavy od okolitého priestoru. Ak základňa pyramídy obsahuje n-uholník, potom počet jej stien je vždy n+1. Z nich je n strán trojuholníkových a jedna strana je spomínaná n-uholníková základňa.
Vrcholy sú body, v ktorých sa pretínajú tri alebo viac stien obrazca. Základná oblasť obsahuje n vrcholov, z ktorých každý je tvorený dvomi trojuholníkovými plochami a základňou. Bod, kde sa stretáva n trojuholníkových strán, sa nazýva vrchol pyramídy. Uvažovaný obrazec teda pozostáva z n+1 vrcholov.
Okraje sú rovné čiary, ktoré sa objavia pri pretínaní dvoch plôch. Každá hrana je na svojich koncoch ohraničená dvoma vrcholmi. Každá pyramída s n-uholníkovou základňou obsahuje 2n hrán. Polovica tohto čísla, teda n, je tvorená výlučne priesečníkom bočných trojuholníkov.
Možné typy figúrok
Názov uvažovanej postavy je jednoznačne určený typom polygónu na základni. Napríklad, ak má pyramída tri rohy a tri strany, potom bude pyramída trojuholníková, ak štyri - štvoruholníková atď.
Mnohouholník môže byť konvexný a konkávny, ako aj pravidelný a všeobecný typ. To všetko určuje aj vzhľad pyramídy.
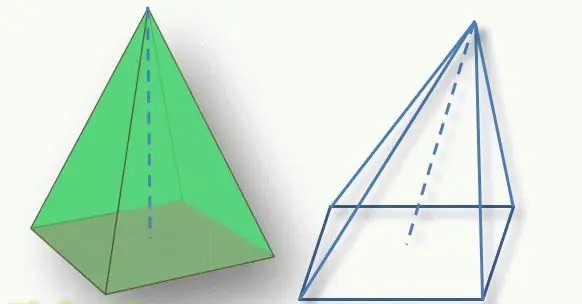
Dôležitým bodom pri určovaní typu postavy je poloha vrcholu pyramídy vzhľadom na jej základňu. Kolmý segment nakreslený zhora k polygonálnej základni sa nazýva výška postavy. Ak tento segment pretína základňu v jej geometrickom strede (pre trojuholník je to priesečník stredov, pre štvoruholník priesečník uhlopriečok), potom sa obrazec nazýva priamka. Inak hovoria o naklonenej pyramíde.
Ak je n-uholník základne pravidelný (rovnostranný trojuholník, štvorec atď.) a útvar je rovný, potom sa nazýva pravidelná pyramída.
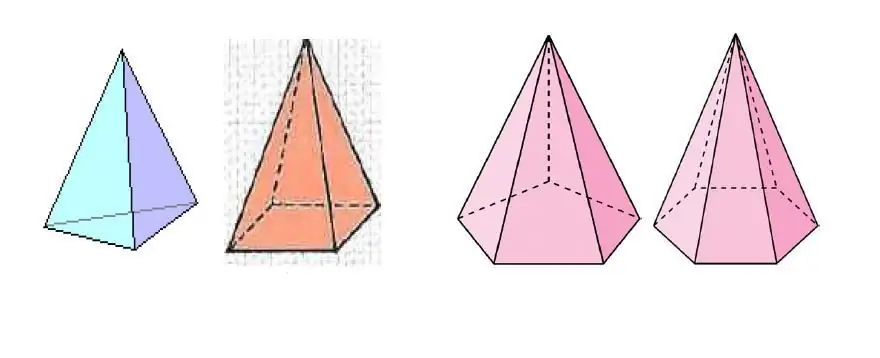
Na obrázku vyššie je niekoľko pyramíd, ktoré sa líšia počtom strán polygónu na základni.
Vlastnosti pravidelných pyramíd
Tieto pyramídy sa líšia od ostatných figúrok tejto triedy vysokou mierou symetrie. V tomto ohľade je vhodné s nimi vykonávať rôzne geometrické výpočty, napríklad objem alebo povrch.
Pravidelná pyramída obsahuje na svojej základni n-uholník, ktorého plocha je jednoznačne určená na základe znalosti dĺžky jej strany. Bočná plocha obrázku je tvorená n rovnakými trojuholníkmi, ktoré sú rovnostranné. Okraje pravidelnej pyramídy umiestnenej na bočnom povrchu sú si navzájom rovné. Hodnota dĺžky tejto hrany sa často používa pri výpočte apotémy obrazca a určovaní plochy povrchu.
Výška pravidelnej pyramídy je druhou dôležitou charakteristikou postavy (prvou je dĺžka hranydôvody). Výška sa používa pri výpočte objemu.
Akákoľvek rovina rovnobežná so základňou, ktorá pretína bočné steny pyramídy, vedie k vytvoreniu mnohouholníkového rezu. Je homotetický vzhľadom na základný polygón. Opísaná operácia rezu vedie k vytvoreniu celej triedy nových figúrok - zrezaných pravidelných pyramíd.
Najznámejšie pyramídy

Samozrejme, toto sú pravidelné štvoruholníkové pyramídy egyptských faraónov. Na mieste zvanom Gíza sa nachádza viac ako 100 týchto kamenných pamiatok, ktorých dokonalosť prevedenia a presnosť geometrických parametrov vedcov neprestáva udivovať dodnes. Najväčšou z nich je Cheopsova pyramída, ktorá je vysoká asi 146 metrov a dlhá asi 230 metrov.
Na čo presne tieto pyramídy slúžili, ako aj akými mechanizmami a kedy boli postavené, dodnes nikto nevie.






