V termodynamike je pri štúdiu prechodov z počiatočného do konečného stavu systému dôležité poznať tepelný efekt procesu. S týmto efektom úzko súvisí pojem tepelná kapacita. V tomto článku sa budeme zaoberať otázkou, čo znamená izochorická tepelná kapacita plynu.
Ideálny plyn
Ideálny plyn je plyn, ktorého častice sa považujú za hmotné body, to znamená, že nemajú rozmery, ale majú hmotnosť, a v ktorom všetka vnútorná energia pozostáva výlučne z kinetickej energie pohybu molekúl a atómy.
Akýkoľvek skutočný plyn v ideálnom prípade nikdy nebude spĺňať popísaný model, pretože jeho častice majú stále nejaké lineárne rozmery a vzájomne interagujú pomocou slabých van der Waalsových väzieb alebo chemických väzieb iného typu. Pri nízkych tlakoch a vysokých teplotách sú však vzdialenosti medzi molekulami veľké a ich kinetická energia niekoľkonásobne prevyšuje potenciálnu energiu. To všetko umožňuje aplikovať s vysokou mierou presnosti ideálny model pre skutočné plyny.
Vnútorná energia plynu
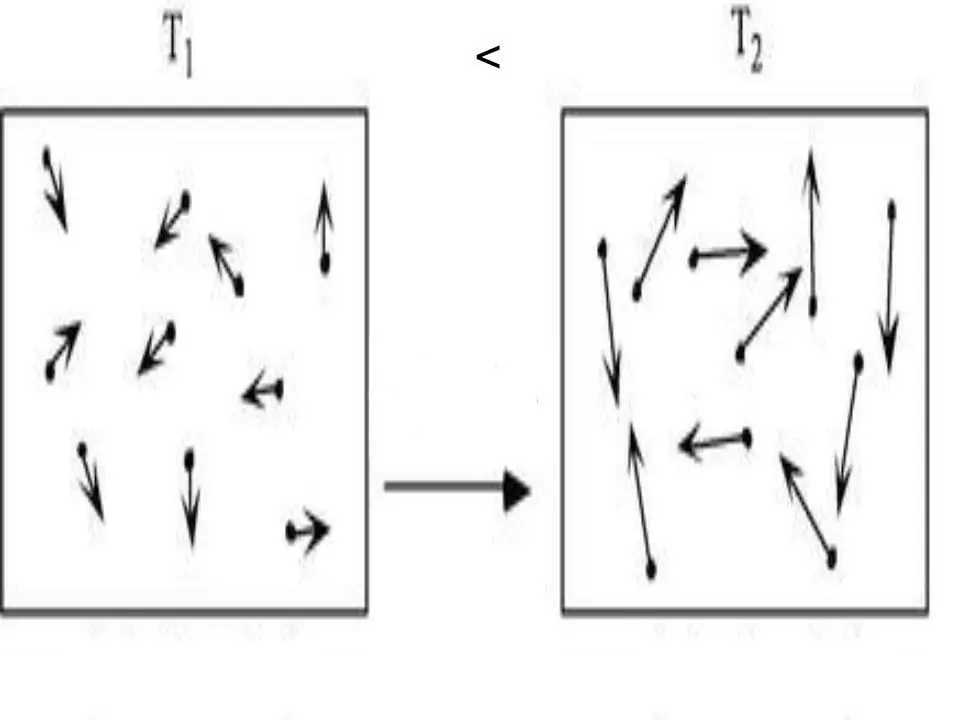
Vnútorná energia každého systému je fyzikálna charakteristika, ktorá sa rovná súčtu potenciálnej a kinetickej energie. Keďže potenciálna energia môže byť v ideálnych plynoch zanedbaná, môžeme pre ne napísať rovnosť:
U=Ek.
Kde Ek je energia kinetického systému. Použitím molekulárnej kinetickej teórie a uplatnením univerzálnej Clapeyronovej-Mendelejevovej stavovej rovnice nie je ťažké získať výraz pre U. Je napísané nižšie:
U=z/2nRT.
T, R a n sú absolútna teplota, plynová konštanta a množstvo látky. Hodnota z je celé číslo označujúce počet stupňov voľnosti, ktoré má molekula plynu.
Izobarická a izochorická tepelná kapacita
Vo fyzike je tepelná kapacita množstvo tepla, ktoré sa musí poskytnúť skúmanému systému, aby sa zohrial o jeden kelvin. Platí aj opačná definícia, to znamená, že tepelná kapacita je množstvo tepla, ktoré systém uvoľní pri ochladení o jeden kelvin.
Najjednoduchším spôsobom systému je určiť izochorickú tepelnú kapacitu. Chápe sa ako tepelná kapacita pri konštantnom objeme. Keďže systém v takýchto podmienkach nevykonáva prácu, všetka energia sa vynakladá na zvyšovanie vnútorných energetických zásob. Označme izochorickú tepelnú kapacitu symbolom CV, potom môžeme napísať:
dU=CVdT.
To znamená zmena vnútornej energiesystému je priamo úmerná zmene jeho teploty. Ak tento výraz porovnáme s rovnosťou napísanou v predchádzajúcom odseku, dostaneme sa k vzorcu pre CV v ideálnom plyne:
СV=z/2nR.
Táto hodnota je v praxi nepohodlná, pretože závisí od množstva látky v systéme. Preto bol zavedený pojem špecifická izochorická tepelná kapacita, teda hodnota, ktorá sa počíta buď na 1 mol plynu alebo na 1 kg. Označme prvú hodnotu symbolom CV, druhú - symbolom CV m. Pre nich môžete napísať nasledujúce vzorce:
CV=z/2R;
CVm=z/2R/M.
Tu je M molárna hmotnosť.
Izobarická je tepelná kapacita pri udržiavaní konštantného tlaku v systéme. Príkladom takéhoto procesu je expanzia plynu vo valci pod piestom, keď sa zahrieva. Na rozdiel od izochorického procesu sa počas izobarického procesu teplo dodávané do systému spotrebuje na zvýšenie vnútornej energie a na vykonanie mechanickej práce, to znamená:
H=dU + PdV.
Entalpia izobarického procesu je výsledkom izobarickej tepelnej kapacity a zmeny teploty v systéme, to znamená:
H=CPdT.
Ak uvažujeme expanziu pri konštantnom tlaku 1 mól plynu, potom prvý zákon termodynamiky bude napísaný ako:
CPdT=CV dT + RdT.
Posledný člen sa získa z rovniceClapeyron-Mendelejev. Z tejto rovnosti vyplýva vzťah medzi izobarickými a izochorickými tepelnými kapacitami:
CP=CV + R.
Pre ideálny plyn je špecifická molárna tepelná kapacita pri konštantnom tlaku vždy väčšia ako zodpovedajúca izochorická charakteristika o R=8, 314 J/(molK).
Stupne voľnosti molekúl a tepelnej kapacity
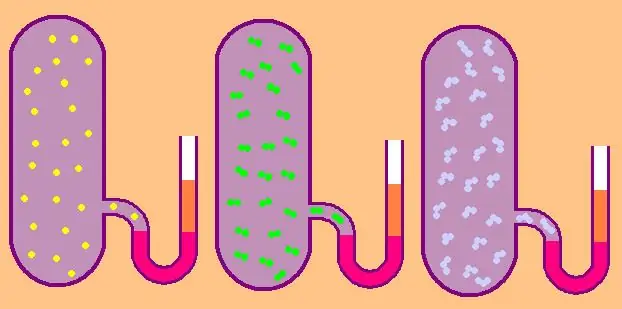
Znova napíšme vzorec pre špecifickú molárnu izochorickú tepelnú kapacitu:
CV=z/2R.
V prípade monatomického plynu je hodnota z=3, pretože atómy v priestore sa môžu pohybovať iba v troch nezávislých smeroch.
Ak hovoríme o plyne pozostávajúcom z dvojatómových molekúl, napríklad kyslík O2 alebo vodík H2, potom, okrem translačného pohybu sa tieto molekuly môžu stále otáčať okolo dvoch vzájomne kolmých osí, to znamená, že z sa bude rovnať 5.
Pre zložitejšie molekuly použite z=6. na určenie CV






