Pri partnerskom hodnotení, napríklad pri hodnotení konkurencieschopnosti produktov, je potrebné, ako pri každej vedeckej práci, vykonávať štatistické spracovanie údajov. Tá začína určením súladu znaleckých posudkov, ktorých číselným vyjadrením je koeficient zhody.
Prečo potrebujeme odborné posúdenie konsenzu?
Toto hodnotenie je potrebné predovšetkým preto, že názory odborníkov sa môžu na odhadované parametre značne líšiť. Na začiatku sa hodnotenie vykonáva tak, že sa indikátory zoradia a priradia sa im určitý koeficient významnosti (váha). Nekonzistentné poradie vedie k tomu, že tieto koeficienty sú štatisticky nespoľahlivé. Názory odborníkov s ich požadovaným počtom (viac ako 7-10) by mali byť distribuované podľa bežného zákona.
Koncept koeficientu zhody
Takže. Súlad je súlad. Koeficient je bezrozmerná veličina ukazujúca pomer disperzie k maximálnej disperzii vo všeobecnom prípade. Zovšeobecnme tieto pojmy.
Koeficient zhody je číslo od 0 do 1, ktoré vyjadruje konzistentnosť znaleckých posudkov, keďporadie niektorých nehnuteľností. Čím je táto hodnota bližšie k 0, tým je konzistencia považovaná za nižšiu. Ak je hodnota tohto koeficientu menšia ako 0,3, názory znalcov sa považujú za rozporuplné. Keď je hodnota koeficientu v rozsahu od 0,3 do 0,7, konzistencia sa považuje za priemernú. Hodnota väčšia ako 0,7 sa považuje za vysokú konzistenciu.
Prípady použitia
Pri vykonávaní štatistického výskumu môžu nastať situácie, v ktorých môže byť objekt charakterizovaný nie dvomi postupnosťami, ktoré sú štatisticky spracované pomocou koeficientu zhody, ale niekoľkými postupnosťami, ktoré sú podľa toho zoradené odborníkmi s rovnakou úrovňou profesionalita v určitej oblasti.
Na potvrdenie správnosti hypotézy, že experti robia relatívne presné merania, je potrebné určiť konzistentnosť hodnotenia, ktoré vykonávajú experti, čo umožňuje vytváranie rôznych zoskupení v expertných skupinách, ktoré sú do značnej miery determinované ľudským faktorom, predovšetkým ako rozdiely v názoroch, koncepciách, rôznych vedeckých školách, povahe profesionálnej činnosti atď.
Stručný popis metódy hodnotenia. Jeho výhody a nevýhody
Pri hodnotení sa používa metóda hodnotenia. Jeho podstata spočíva v tom, že každá vlastnosť objektu má pridelenú svoju špecifickú hodnosť. Navyše, každému odborníkovi zaradenému do expertnej skupiny je táto hodnosť pridelenásamostatne, z čoho vyplýva potreba spracovávať tieto údaje za účelom zistenia súladu znaleckých posudkov. Tento proces sa vykonáva výpočtom koeficientu zhody.
Hlavnou výhodou metódy hodnotenia je jej jednoduchá implementácia.
Hlavné nevýhody metódy sú:
- malý počet hodnotených objektov, pretože keď ich počet presiahne 15-20, je ťažké priradiť hodnotenie cieľov;
- Na základe použitia tejto metódy zostáva otvorená otázka, ako ďaleko sú od seba skúmané objekty vo význame.
Pri použití tejto metódy je potrebné vziať do úvahy, že hodnotenia sú založené na nejakom druhu pravdepodobnostného modelu, takže vzhľadom na rozsah ich treba používať opatrne.
Kendallov koeficient zhody
Používa sa na určenie vzťahu medzi kvantitatívnymi a kvalitatívnymi znakmi charakterizujúcimi homogénne objekty a zoradených podľa rovnakého princípu.
Tento koeficient je určený vzorcom:
t=2S/(n(n-1)), kde
S - súčet rozdielov medzi počtom sekvencií a počtom inverzií na druhom prvku;
n - počet pozorovaní.

Algoritmus výpočtu:
- Hodnoty x sú zoradené vzostupne alebo zostupne.
- Hodnoty y sú usporiadané v poradí, v akom zodpovedajú hodnotám x.
- Pre každú nasledujúcu hodnosť y určite, koľko vyšších hodnôt hodnosti bude nasledovať. Sčítajú sa a vypočíta sa miera korešpondencie postupností poradí v x a y.
- Podobne sa vypočíta počet radov y s nižšími hodnotami, ktoré sa tiež sčítajú.
- Pridajte počet hodností s vyššími hodnotami a počet hodností s nižšími hodnotami, výsledkom čoho bude hodnota S.
Tento koeficient ukazuje vzťah medzi dvoma premennými a vo väčšine prípadov sa nazýva Kendallov koeficient poradovej korelácie. Takáto závislosť môže byť znázornená graficky.
Určenie koeficientu
Ako sa to robí? Ak počet hodnotených znakov alebo faktorov presiahne 2, použije sa koeficient zhody, ktorý je v podstate viacnásobným variantom hodnotovej korelácie.
Buďte opatrní. Výpočet koeficientu zhody vychádza z pomeru odchýlky súčtu druhých mocnín hodností od priemerného súčtu druhých mocnín hodností, vynásobeného 12, ku štvorcu expertov, vynásobeného rozdielom medzi druhou mocninou počtu objektov a počet objektov.
Algoritmus výpočtu
Aby sme pochopili, odkiaľ pochádza číslo 12 v čitateli výpočtového vzorca, pozrime sa na algoritmus určovania.
Pre každý riadok s hodnosťami určitého odborníka sa vypočíta súčet hodností, čo je náhodná hodnota.
Koeficient zhody je všeobecne definovaný ako pomer odhadu rozptylu (D) k maximálnej hodnote odhadu rozptylu(Dmax). Poďme postupne sformulovať definície týchto veličín.
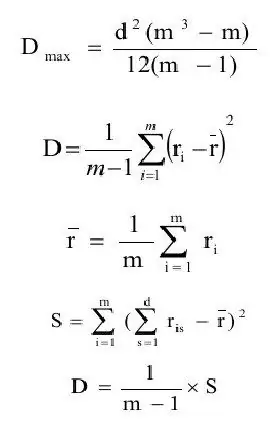
kde ravg - odhad očakávania;
m - počet objektov.
Nahradením výsledných vzorcov vo vzťahu k D k Dmax dostaneme konečný vzorec pre koeficient zhody:
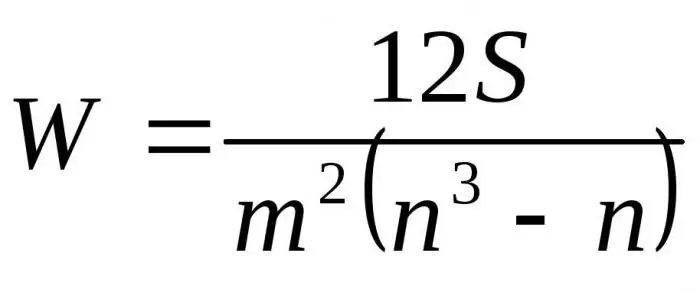
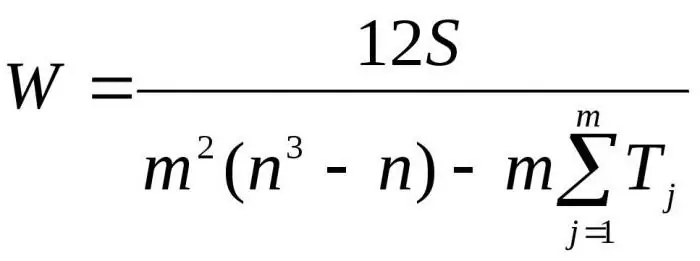
Tu m je počet expertov, n je počet objektov.
Prvý vzorec sa používa na určenie faktora zhody, ak neexistujú žiadne súvisiace poradia. Druhý vzorec sa používa, ak existujú súvisiace hodnosti.
Výpočet koeficientu zhody je teda u konca. Čo bude ďalej? Získaná hodnota sa vyhodnotí z hľadiska významnosti pomocou Pearsonovho koeficientu vynásobením tohto koeficientu počtom expertov a počtom stupňov voľnosti (m-1). Výsledné kritérium sa porovnáva s tabuľkovou hodnotou a ak hodnota prvého prevyšuje posledné, hovorí o význame skúmaného koeficientu.
V prípade príbuzných hodností sa výpočet Pearsonovho kritéria trochu skomplikuje a vykonáva sa pomocou nasledujúceho pomeru: (12S)/(d(m2+ m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Príklad
Predpokladajme, že expertná metóda hodnotí konkurencieschopnosť masla predávaného v maloobchodnej sieti. Uveďme príklad výpočtu koeficientu zhody. Pred hodnotením konkurencieschopnosti je potrebné zoradiť spotrebiteľavlastnosti tohto produktu, ktoré sa zúčastňujú hodnotenia. Predpokladajme, že tieto vlastnosti budú nasledovné: chuť a vôňa, konzistencia a vzhľad, farba, balenie a označovanie, obsah tuku, obchodný názov, výrobca, cena.
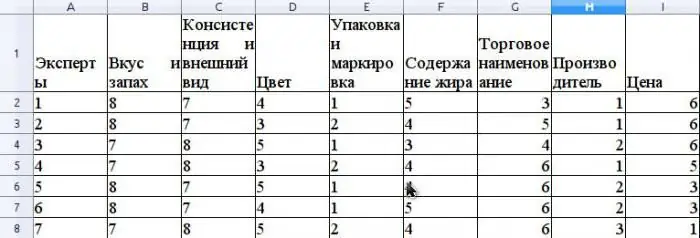
Predpokladajme, že expertná skupina pozostáva zo 7 expertov. Obrázok ukazuje výsledky hodnotenia týchto nehnuteľností.
Priemerná hodnota r sa vypočíta ako aritmetický priemer a bude 31,5. Ak chcete nájsť S, spočítajte druhé mocniny rozdielov medzi ris a priemerom r podľa vzorca vyššie a určite, že hodnota S je 1718.
Vypočítajte koeficient zhody pomocou vzorca bez použitia súvisiacich hodností (hodnotenia by súviseli, ak by mal rovnaký odborný poradca rovnaké hodnosti pre rôzne vlastnosti).
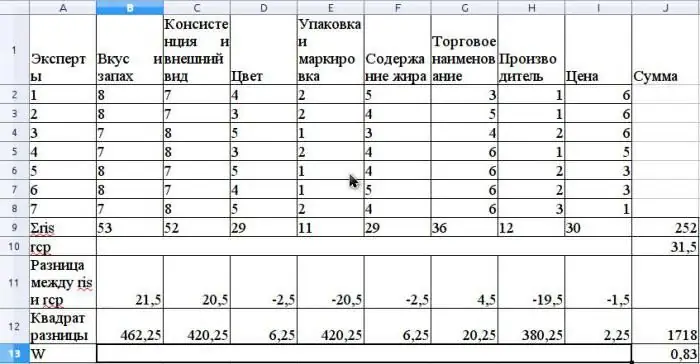
Hodnota tohto koeficientu bude 0,83. To naznačuje silný konsenzus medzi odborníkmi.
Skontrolujte jeho význam pomocou Pearsonovho testu:
7 x 0,83 x (8-1)=40,7.
Pearsonov tabuľkový test na 1% hladine významnosti je 18,5 a na 5% - 14,1..
Príklad demonštruje jednoduchosť a dostupnosť výpočtu pre každého, kto pozná základy matematických výpočtov. Na ich zmiernenie,použite formuláre tabuliek.
Na záver
Koeficient zhody teda ukazuje konzistentnosť názorov viacerých odborníkov. Čím ďalej je od 0 a bližšie k 1, tým sú názory konzistentnejšie. Tieto koeficienty musia byť potvrdené výpočtom Pearsonovho kritéria.






