Zrýchlenie a rýchlosť sú dve dôležité kinematické charakteristiky akéhokoľvek typu pohybu. Poznanie závislosti týchto veličín od času vám umožňuje vypočítať dráhu, ktorú telo prejde. Tento článok obsahuje odpoveď na otázku, ako nájsť zrýchlenie, ak poznáte rýchlosť a čas.
Koncept rýchlosti a zrýchlenia
Skôr ako odpovieme na otázku, ako, keď poznáme rýchlosť a čas, nájsť zrýchlenie, zvážme každú z charakteristík z hľadiska fyziky.
Rýchlosť je hodnota, ktorá určuje rýchlosť zmeny súradníc v priestore pri pohybe tela. Rýchlosť sa vypočíta podľa vzorca:
v=dl/dt.
Kde dl je dráha, ktorú telo prejde za čas dt. Rýchlosť je vždy nasmerovaná pozdĺž dotyčnice na dráhe pohybu.
Pohyb môže prebiehať buď konštantnou rýchlosťou v priebehu času, alebo premenlivou rýchlosťou. V druhom prípade hovoríme o prítomnosti zrýchlenia. Vo fyzike zrýchlenie určuje rýchlosť zmeny v, ktorá je zapísaná ako vzorec:
a=dv/dt.
Táto rovnosť je odpoveďou na otázku, ako ju nájsťzrýchlenie rýchlosti. Na to stačí zobrať prvú časovú deriváciu v.
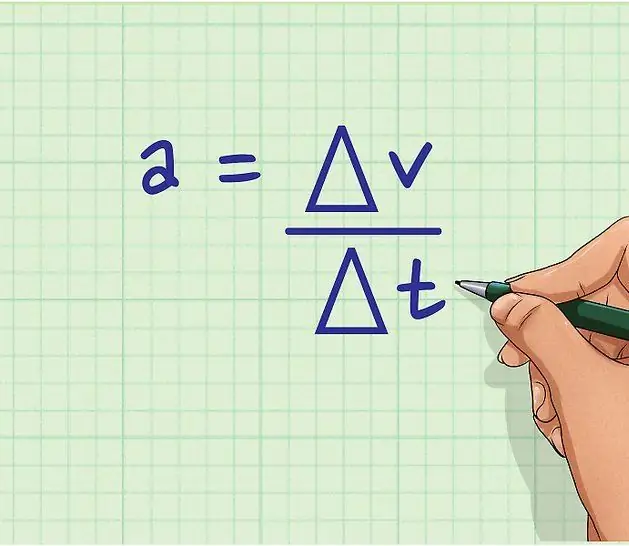
Smer zrýchlenia sa zhoduje so smerom rozdielu vektorov rýchlosti. V prípade priamočiareho zrýchleného pohybu sú veličiny a a v nasmerované rovnakým smerom.
Ako nájsť zrýchlenie pri danej rýchlosti a čase?
Pri štúdiu mechaniky sa najprv uvažuje o rovnomerných a rovnomerne zrýchlených typoch pohybu pozdĺž priamej trajektórie. V oboch prípadoch by sa na určenie zrýchlenia mal zvoliť časový interval Δt. Potom je potrebné určiť hodnoty rýchlostí v1 a v2 na konci tohto intervalu. Priemerné zrýchlenie je definované takto:
a=(v2- v1)/Δt.
V prípade rovnomerného pohybu zostáva rýchlosť konštantná (v2=v1), takže hodnota vôle byť nula. V prípade rovnomerne zrýchleného pohybu bude hodnota a konštantná, takže nezávisí od časového intervalu Δt vo vzorci.
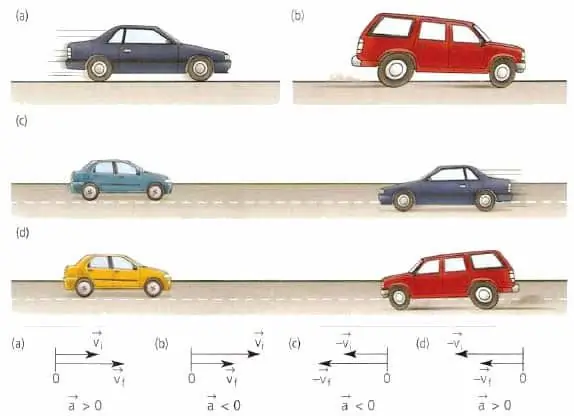
Pre zložitejšie prípady pohybu, keď je rýchlosť funkciou času, by ste mali použiť vzorec pre deriváciu cez prechod, ktorý bol uvedený v odseku vyššie.
Príklad riešenia problému
Po vysporiadaní sa s otázkou, ako nájsť zrýchlenie, poznajúc čas a rýchlosť, vyriešime jednoduchý problém. Predpokladajme, že teleso pohybujúce sa po určitej trajektórii mení svoju rýchlosť v súlade s nasledujúcou rovnicou:
v=3t2- t + 4.
Aké bude zrýchlenie telesa v čase t=5 sekúnd?
Zrýchlenie je prvá derivácia v vzhľadom na premennú t, máme:
a=dv/dt=6t - 1.
Ak chcete odpovedať na otázku problému, mali by ste do výslednej rovnice nahradiť známu hodnotu času: a=29 m/c2.






